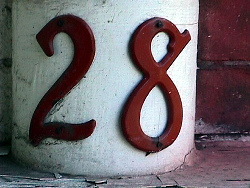23. Every natural number can be unambiguously described in fourteen words or less
You know this can’t be true.
(Here a ‘word’ means an ordinary English word, found in a dictionary.)
After all, there are only finitely many words, so there are only finitely many sentences constructible in fourteen words or less. But there are infinitely many natural numbers! So it can’t be true that every natural number can be unambiguously described in fourteen words or less. Yet here’s a “proof” of the claim. What’s wrong with it?
You know this can’t be true.
(Here a ‘word’ means an ordinary English word, found in a dictionary.)
After all, there are only finitely many words, so there are only finitely many sentences constructible in fourteen words or less. But there are infinitely many natural numbers! So it can’t be true that every natural number can be unambiguously described in fourteen words or less. Yet here’s a “proof” of the claim. What’s wrong with it?
Suppose the claim is false. Then at least one natural number cannot be unambiguously described in fourteen words or less. Call the smallest such number N. Then N is the smallest natural number that cannot be unambiguously described in fourteen words or less, which is a complete and unambiguous fourteen-word description of N. Contradiction.
From math.toronto.edu
Menu
 What’s a logical paradox?
What’s a logical paradox? Achilles & the tortoise
Achilles & the tortoise The surprise exam
The surprise exam Newcomb’s problem
Newcomb’s problem Newcomb’s problem (sassy version)
Newcomb’s problem (sassy version) Seeing and being
Seeing and being Logic test!
Logic test! Philosophers say the strangest things
Philosophers say the strangest things Favourite puzzles
Favourite puzzles Books on consciousness
Books on consciousness Philosophy videos
Philosophy videos Phinteresting
Phinteresting Philosopher biographies
Philosopher biographies Philosopher birthdays
Philosopher birthdays Draft
Draftbarang 2009-2024  wayback machine
wayback machine
 wayback machine
wayback machine