Notes from the underground |
 |
Updated 1 August 2024 |
Newcomb’s problem (sassy version)
Preface
This is a livelier version of my take on Newcomb’s problem. I like this version better as it cuts to the chase and lets me spell out my solution a little more. A basic familiarity with Newcomb’s problem is presupposed. (Written in 2016.)
This is a livelier version of my take on Newcomb’s problem. I like this version better as it cuts to the chase and lets me spell out my solution a little more. A basic familiarity with Newcomb’s problem is presupposed. (Written in 2016.)
1. Personal battle
There is nothing with plausibility that can be said against the plain and simple causal-dominance argument for two-boxing.
I cannot recall when I first heard of Newcomb’s problem but I do remember that the first time it gripped me I was immediately a one-boxer.
That is to say, I was a one-boxer from the start. One-boxing instinctively felt right to me—notwithstanding the evident force of the two-box argument.
This left me with the nagging problem of explaining what then was wrong with the simple and utterly suasive argument for taking both boxes. And this problem seemed to me so interesting that I was soon thinking about it day and night. For me, this has always been the real issue in Newcomb’s problem and what follows is largely an account of my battle with the argument for taking both boxes.
I assume that Newcomb’s problem is understood because I want to jump right in. Here’s a quick statement so that you can see that I’m indeed talking about the standard problem introduced by Robert Nozick in 1969. (“It is a beautiful problem. I wish it were mine.”)
I should make one remark before proceeding. I said above that you believe that the predictor is very likely to have predicted your choice correctly. In what follows, I will often say instead that you believe that the predictor knew which choice you would make. There you are, seated before the boxes, deciding whether to take both boxes or just box B. Ordinarily, you would simply take both boxes since, regardless of what box B contains, you’ll get a thousand dollars more by doing so. The fly in the ointment is your belief that the predictor knew in advance which choice you would make. More on this fly below; my present remark is just that this is not how the predictor in question is normally described, viz., as someone who knew what you were going to do. He is more often characterized as someone who is very good at predicting what people will do, or as someone who typically tends to get his predictions right, or as someone with an uncanny ability to anticipate your choices, and so on.
I don’t think very much hangs on this however. My main reason for speaking of the predictor as knowing what you will do is that later I will describe a case involving a father who wishes to offer his daughter a choice between two gifts on her birthday but knows in advance which gift she will choose. This is meant to be an ordinary description of a sort of case with which we are all familiar—a case of “foreknowledge”—and it is perfectly natural to use the word ‘know’ in this sort of context. I will then compare this man to the predictor in Newcomb’s problem. So the predictor knows which choice you will make in the same sense that the man knows which gift his daughter will choose. Speaking in this ordinary way will make some of what I say below much easier to understand. (I will revisit this point at the end.)
Someone might question whether anyone could ever know what they were going to do in such a situation as Newcomb’s. If so, they can resolve Newcomb’s problem by pointing this out – no predictor could ever know what they were going to do any more than any father (say) could ever know what his daughter was going to do! The ensuing contradiction between the argument for taking both boxes and the argument for taking just box B can then be traced back to the “absurd” supposition that the predictor knew what they were going to do. I don’t know of anyone who thinks that this is a good way to resolve Newcomb’s problem though. There is a better way.
So how do we resolve Newcomb’s problem? I mentioned that I was a one-boxer from the start and that, for me, the real problem has always been to explain what was wrong with the simple and suasive argument for taking both boxes.
So I’m going to say very little about the case for taking just box B in what follows. I think that this case is basically sound. If you have every reason to believe that the predictor knows what you will do, then you have every reason to expect a million dollars if you take just box B as opposed to a mere $1,000 if you take both boxes. You thus have every reason to take just box B. This states the case in plain language. Were more precision required, a one-boxer could appeal to a traditional “expected-utility” calculation—a kind of mathematical calculation whose details I assume are familiar. I will say something about this towards the end, but bear in mind that I’m not really concerned with the one-box argument in this essay. I want rather to expose what I think is the flaw in the argument for taking both boxes. As I said, this is the story of my battle with the two-box argument.
Some people place little faith in philosophical instincts when it comes to these sorts of things, but I’m not one of them. I believe that one can often have a “nose” for the right way to go. In a game of chess, a player can often have a nose for whether to move his bishop or knight in a difficult position without being able to fully explain his decision. In philosophy, one can likewise have a nose for the right path to follow. My nose has always told me that something is wrong with the argument for taking both boxes, the question only being to pin it down. So let me turn to this argument at once.
2. The two-box argument
The case for taking both boxes can be made in many ways. People sometimes invoke technical apparatus like dominance reasoning or causal decision theory to show that it is better to take both boxes but I tend to find that plain language is sufficient. Newcomb’s problem has always gripped me in plain language and I have always sought to resolve the difficulty likewise. Thus, as the boxes stand before you, it is obvious that there is more money in both boxes than in box B alone. This cannot be reasonably denied. In fact, it cannot be denied at all. Regardless of what the man has predicted, regardless of how accurate he is, and regardless of what he has placed in box B, you know that there is more money in both boxes than in box B alone. Indeed, you know that there is exactly a thousand dollars more. It follows that you will get more money (a thousand dollars more) by taking both boxes than by taking box B alone. Since money is your aim, you must accordingly do so.
This simple argument bothered me so much that I dropped everything and started thinking about it day and night.
I felt that something had to be wrong with it but for the life of me couldn’t see what. You can pick at the argument in various obvious ways but it’s not easy to find anything convincing to say against it. And I wanted something convincing, something you could feel in your bones.
Consider for example the “fly in the ointment” mentioned above – your belief that the predictor knew which choice you would make. The most glaring thing about the two-box argument is that it ignores this aspect of the problem completely. The predictor does not even get a mention! This is most disconcerting. Surely this is the error in the two-box argument, viz., that it ignores a feature of the problem—the predictor’s powers—that is obviously relevant to your eventual decision?
This is a natural objection to make and essentially the first one that anyone thinks of. But you don’t have to look very far to see that it is not (ultimately) very convincing. It is true that the two-boxer ignores a feature of the problem that seems to be relevant, viz., the powers of the predictor. But a similar charge can be levelled against the one-boxer! What the one-boxer ignores is the plain fact that, as the boxes stand before him, there is more money in both boxes than in box B alone. This feature of the problem also seems to be relevant to your eventual decision. And the one-boxer doesn’t even mention it! So this is a case of the pot calling the kettle black – not very convincing.
The truth is that Newcomb’s problem contains two prominent features, both of which seem to be relevant, but which pull curiously in opposite directions. To have a balanced view of the problem, we must be sensitive to both features. If you focus on the powers of the predictor, then it can easily seem that taking box B alone is better. (Given his powers, you will get a million dollars if you take box B alone but just $1,000 if you take both boxes.) But if you focus on the fact that—as the boxes stand before you—there is more money in both boxes than in box B alone, then it can easily seem that taking both boxes is better. (If there is more money in both boxes, then you will get more money if you take both boxes.) Are we to say that one of these features is more relevant to your decision than the other? But which one and why? Offhand, there seems to be no saying.
In a pair of famous papers written in 1981 and 1985, the philosopher Terence Horgan analyzed this very issue in detail and came away empty-handed. “Stalemate” was his conclusion, meaning that he could see no way to privelege either of the two mentioned features over the other. Horgan himself favoured one-boxing, it is worth mentioning, and attempted (at first) to argue that the powers of the predictor were a more important consideration than the fact that there was more money in both boxes. Indeed, his initial paper was so dazzling that it won a prize for being one of the best philosophy papers of the year. But he turned around and conceded in his second paper that there was no good way after all to make the case. And I think ultimately that this is true. There is no real point in trying to argue that either of the two mentioned features is more important than the other. What we need rather is a way of looking at Newcomb’s problem that embraces both features simultaneously.
Before explaining how I think this can be done—and how the resulting picture reveals (in my opinion) where the two-box argument really goes wrong—let me explain how another philosopher thought this could be done. This other philosopher was David Lewis. Unlike me, Lewis was a two-boxer and felt that there was nothing wrong with the two-box argument at all. So his overall picture of things is going to be very different from mine. But this doesn’t matter for now: the important thing is to appreciate how it is possible to think about Newcomb’s problem in such a way that both of the aforementioned features of the problem are accommodated at once.
As mentioned, Lewis believed that it was better to take both boxes than to take box B alone. He believed that you would get more money by doing so, i.e., because there is more money in both boxes. This accommodates the one feature of our problem. But Lewis did not ignore the powers of the predictor either. To accommodate them, he attempted to “make sense” of the fact that one-boxers in this game tend to end up with more money than two-boxers. Note that this fact is not in dispute and is essentially built into the problem. (If the fact did not hold, the predictor’s powers would be in question, and they are not supposed to be in question.) But Lewis did not think that the fact showed that one-boxing was the right thing to do. He interpreted it as showing rather that the predictor was (for some reason) rewarding irrational people!
This sounds like a joke at first, but only at first. To see Lewis’s point, it helps to imagine a case where it is clear that the predictor is rewarding irrational people. It helps to see that such a thing is possible and that Lewis was not simply grasping at straws. So imagine a predictor who can tell in advance whether someone is rational or irrational. Whenever he meets a rational person, he presents her with two open boxes A and B, where A contains $1,000 and B contains nothing. The amounts in the boxes are plain to see and the subject is invited to take either both boxes or box B alone. Being rational, she naturally takes both boxes on the (correct) grounds that she gets more money that way. Irrational people are likewise presented with two open boxes A and B, but this time A contains $1,000 and B contains a million dollars. They too may take either both boxes or just box B and the amounts in the boxes are again plain to see. Being irrational, they take just box B on the (silly) grounds that they get less money that way. Note that, in either case, taking both boxes is the rational thing to do; it is just that irrational people fail to see this. Nevertheless, they end up with a million dollars whereas rational people get just $1,000. In this case, it seems clear that the predictor is (for some reason) rewarding irrational people.
Lewis believed that something like this was going on in Newcomb’s problem, except of course in a more subtle way. He recommended this view in a short paper in 1981, after the suggestion was first made by the philosophers Gibbard & Harper in a longer and more technical paper in 1978. The upshot was that two-boxers could now take both boxes “in good conscience,” as it were. For here was a way of embracing the predictor’s powers while maintaining that taking both boxes was the rational thing to do. It should be emphasized, as Lewis himself did, that none of this shows that taking both boxes is the rational thing to do in Newcomb’s problem and that taking just box B is irrational. The point is only that the two-boxing position is overall coherent: it can accommodate all the relevant features of the problem. In particular, the objection that the two-boxer ignores the powers of the predictor is now completely defanged. So if you are independently persuaded that taking both boxes is the right thing to do, this way of looking at the matter can be recommended.
Not me, however. I was independently persuaded that taking just box B was correct. So I had the opposite problem from Lewis, Gibbard and Harper. I needed a way of looking at things that accommodated the fact that there was obviously more money in both boxes than in box B alone. How does a one-boxer take just box B in the face of this fact?
After thinking for a considerable time—many months, if the truth be told—the answer finally came to me. Not only did I understand how to one-box “in good conscience,” I also understood what was wrong with the argument for taking both boxes.
3. A more natural variant
To explain this, it helps to consider a simple variant of Newcomb’s problem. Traditionally, your choices are between taking both boxes and box B alone – an honoured tradition I have observed so far. But this way of putting it can be a little confusing. It is more natural to have a choice between taking the one box or the other. It is not hard to set this up, so let’s do it. This is what I did in the course of things and it helped me see what was wrong with the two-box argument.
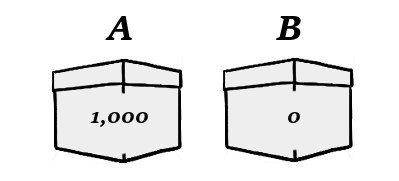
In this variant, there are still two boxes A and B, but your choices are simply between taking box A (alone) and taking box B (alone). This is slightly more natural. And now, if the man predicted that you would take box A, then he has (already) placed $1,000 in A and nothing in B. Like this:
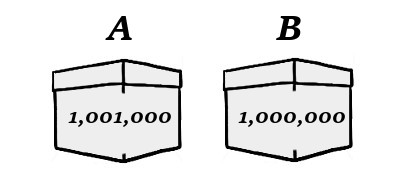
On the other hand, if he predicted that you would take box B, then he has (already) placed a million-and-a-thousand dollars in A and a million dollars in B. Like this:
One of these situations is yours but you have no idea which one. (The boxes are opaque.) Note that box B contains either nothing or a million dollars and, in either case, box A contains a thousand dollars more. You may take either box A or box B in the knowledge of the facts just stated and the belief that the man knew which box you would take. Which box should you take?
A traditional one-boxer would take box B whereas a traditional two-boxer would take box A. (I hope this is obvious.) And my instincts indeed tell me that I should take box B. (“If the predictor knew what I would do, then if I take box B, he will have placed me in the second situation and I will get a million, whereas if I take box A, he will have placed me in the first and I will get just $1,000.”) But it is hard to ignore the simple case for taking box A, which is that, in either situation, box A contains more money than box B. So, no matter which situation the man has placed me in, I should take box A!
In terms of this variant, my goal is to explain how someone can sensibly (“in good conscience”) take box B despite knowing that box A contains more money! As it turns out, the explanation will also show where the argument for taking box A goes wrong. Everything I say below can easily be adapted to the traditional version of Newcomb’s problem.
4. Father and daughter
I can now introduce the father who wishes to give his daughter a choice between two gifts on her birthday. As mentioned, I will eventually compare this father with the predictor in Newcomb’s problem.
Suppose that the gifts in question are an anklet (A) and a bracelet (B): the father is letting his daughter choose one of these as a birthday gift. For our purposes, imagine that the father presents his daughter with two gift-wrapped boxes, e.g., as pictured above. (He has purchased both gifts in advance and has wrapped each in a box of its own.) The boxes are labelled A and B, with the obvious meanings, and the daughter is invited to choose between the anklet and the bracelet by picking the appropriately-labelled box.
In an ordinary case, the girl would just make her choice—the anklet, say—and pick the appropriate box: A, in this case. The father would then have to “dispose” of the gift she did not choose—the bracelet—e.g., by sending it back to the store for a refund.
But suppose that the father knows in advance that his daughter will choose the anklet over the bracelet – a case of “foreknowledge.” How does the father know this? Well, we can just suppose that he knows his daughter well. (We needn’t suppose that she told him as much.) Here’s the question that I really want to pursue: in this case, does the father really need to procure the bracelet in advance and place it in box B? He knows, we are supposing, that his daughter is not going to pick the bracelet, so it seems fair to ask why he should trouble himself to purchase it knowing that he will eventually have to return it to the store for a refund? There is a case here for saying that he doesn’t really need to get the bracelet in advance. He does need to get the anklet and place it in box A, of course, since he knows that his daughter is going to choose it. But I don’t see that he needs also to get the bracelet to be able to sincerely offer her a choice between the anklet and the bracelet on the day in question.—At least, this is what I plan now to argue.
Let me make things clear before proceeding. Here is a girl, presented with two opaque boxes A and B. Her father offers her a choice between an anklet and a bracelet and invites her to pick the appropriately-labelled box. She thinks for a while and then picks box A, just as her father knew she would. She thereby gets an anklet. Unknown to her, box B is empty. It does not contain a bracelet because her father reasoned that, since he knew that she was not going to choose the bracelet over the anklet, he need not bother getting it. The father then simply disposes of the empty box B, glad to have saved himself the trouble of returning to the store a bracelet that he knew she was not going to pick. And the question I’m asking is this: did the girl really have a choice between an anklet and a bracelet in the situation as described? In particular, did her father deprive her of that choice by failing to procure the bracelet?
I’m going to try to persuade you that the answer to the last question is no. Notwithstanding that no bracelet is anywhere in the vicinity, and we may even imagine that all bracelets have been sold out by now, and even that the father foresaw that this would be so, he did not deprive his daughter of the choice in question by failing to procure the bracelet, i.e., by leaving box B empty. This is essentially because he knew that she would not choose the bracelet anyway.
Before trying to persuade you of this, let me address three questions that sometimes arise when I bring this example up with friends.
First, if the father already knows that his daughter will choose the anklet over the bracelet, why bother with this rigamarole of giving her a choice between the two. Why not just give her the anklet on her birthday and be done with it?
Well, let me first say that the rigamarole will eventually help me compare the situation with Newcomb’s problem, with its two boxes and so on.—But never mind this for now, because we can also answer the question on its own terms. Suppose that the father wants his daughter to make the choice anyway because he believes that she will value the gift more if it is of her own choosing (say). Lots of people believe some such thing and the father could easily be one of them. Or we could tell a longer story. Suppose that it is a hallowed tradition in this family that every daughter on her sixteenth birthday shall be given a choice between an anklet and a bracelet and it is the youngest daughter’s turn. The father is bound to tradition and so must present the choice to his daughter notwithstanding that he already knows which gift she will choose. So there are any number of reasons why the rigamarole might be necessary, apart from my desire to connect the case with Newcomb’s problem. Note also that I’m assuming that you can meaningfully ask someone to choose between two options even though you already know which option they will choose. This is the familiar philosophical assumption that foreknowledge of choice is compatible with freedom of choice. This assumption is widely accepted and I won’t feel the need to defend it here, especially since the assumption is also made in the context of Newcomb’s predictor and usually allowed without question. (The predictor knows what you will do, but you have a free choice in the matter anyway.) I will say a little more about this “compatibilism” below.
Second, one can wonder whether the father needs to bother with two boxes if he is going to leave one of them empty. If he has decided not to procure the bracelet (on the grounds explained above), then why bother with the second box at all, which shall after all simply remain empty? Why not just present his daughter with one gift-wrapped box, containing the anklet, and invite her to choose between the anklet and the bracelet before opening the box? Or why not just hold the anklet behind his back, invite her to make the choice between the anklet and the bracelet, and then present her with the anklet when she chooses it, as he knows she will. The answer is that either of these alternatives is (ultimately) also acceptable. In either of these cases too, I would say that the father does not deprive his daughter of the choice between the anklet and the bracelet, as will be clear from my discussion below. Again, I’m telling the story with two boxes mainly because it makes the comparison with Newcomb’s problem easier.
Finally, one might ask if it makes a difference if the daughter were to realize that one of the boxes before her was empty. The way I’m telling the story, the father leaves one of the boxes empty without alerting his daughter to this fact. Suppose however that the daughter (somehow) catches on to what her father has done. So she knows that, while one of the two boxes before her contains the gift her father is expecting her to choose, the other box is simply empty. And yet she is being asked to “choose” between the two gifts. Will she not vehemently protest that no such choice is before her and that she has no choice but to take the gift her father has bought, since the other gift is not available for her taking? Well, this is exactly the question I wish to pursue so we can turn to this at once. For the purposes of the story, it helps if the daughter is not made aware of the situation since this introduces unnecessary complications concerning her reaction and behaviour that are not relevant to the point I wish to make. I will revisit these complications when I compare the father to Newcomb’s predictor as they will be more relevant then. For the moment, let us assume that the daughter does not realize that one of the boxes before her is empty.
5. A question of choice
And so—finally—does the daughter really have a choice between an anklet and a bracelet in the situation as described? In particular, has the father robbed her of that choice by procuring just the anklet—the gift he knows she will choose—while deliberately neglecting to procure the bracelet?
From my experience, a natural first reaction is that the father has indeed robbed his daughter of the choice in question by his somewhat cavalier behaviour. One thinks: for the choice between the anklet and the bracelet to be genuinely before her, both gifts must be available for her taking. But the father has made one of them (the bracelet) unavailable, thereby robbing her of the choice between the two. And so, whether she realizes it or not, the girl really has no choice but to take the only gift that her father has procured—the anklet, as we are supposing. The choice of the bracelet is not really before her!
I said above that I hold the opposite view, and so I think that this natural reaction is mistaken. But let me first mention a slightly different case for which I think such a reaction would be appropriate. Suppose that the father doesn’t really know which gift his daughter will choose but decides for some reason to guess. He guesses that she will choose the anklet (say) and decides bravely to purchase it alone. The rest of the story is then as before: he presents her with two boxes A and B, where A contains the anklet and B is empty. The daughter chooses box A and is pleased to receive the anklet. And the father simply throws away the empty box B. In this case, I’d be the first to agree that the father did rob his daughter of the choice between the anklet and the bracelet. Notwithstanding that the girl goes away pleased, she had no real choice but to take the anklet and the father was just lucky to get away with it.
This case of course is not the same as ours. In our case, the father doesn’t just guess that his daughter will choose the anklet but knows that she will do so. Does this make a difference? I think that it does: that the girl ends up choosing the anklet—the only gift her father has brought to the table—is now no longer a matter of luck. We cannot now rail that the father was “lucky to get away with it.” Luck is no longer at issue because he knew that she would not choose the bracelet. As such, his failure to procure the bracelet can no longer be grounds for censure. Or so it seems to me! I find it useful to put the matter in this way, in terms of whether the father’s failure to procure the bracelet occasions any censure—because it is easier to have an opinion on this question. Moreover, if we agree that it does not, then I think we should agree that his daughter was not for that reason deprived of the choice between the anklet and the bracelet. But there is no other reason (in our story) why she should have been so deprived. This is what satisfies me that she has not been deprived of the choice in question at all. In this sense, the choice between the anklet and the bracelet remains open to her despite the fact that the bracelet is not available for her taking.
This states the essential case, but I guess I should say a little more since everything is going to hang on this before long!
In the case described, where the father neglects to procure the bracelet in the knowledge that his daughter will choose the anklet, there is perhaps an obvious underlying worry. This concerns what would happen were his daughter to choose the bracelet. The father knows that she will not but we can still ask what would happen if she did? Given that no bracelet is available for her taking, it is clear what the answer must be. Were she to choose the bracelet, she would not get it! (She would pick box B and find it to be empty.) But how then can the choice of the bracelet be said to be before her? Surely a necessary condition for something to be among your choices is that you will get it if you choose it?
The answer to this worry is not hard to see. If the father knows that his daughter will not choose the bracelet, then it is no longer appropriate to draw any conclusions by considering what would happen were she to do so. What would happen becomes irrelevant because the father can “set things up” in any way he likes, safe in the knowledge that she will not choose the bracelet. For instance, suppose that, instead of leaving box B empty, he places a stone in it, just for weight. Does this mean that, in choosing between box A and box B, his daughter is choosing between an anklet and a stone? After all, if she were to pick box A, she would receive an anklet, but if she were to pick box B, she would receive a stone! So, in choosing between the boxes, she must really be choosing between an anklet and a stone—whether she knows this or not! It seems to me however that only a superficial thinker would draw this conclusion. Once we understand that the contents of box B are up to the father, and that he knows that his daughter will not pick that box, it becomes clear that it means nothing to consider what would happen if she were to pick it. For, as I said, the father can put anything he likes in box B, safe in the knowledge that she will not choose it. So no meaningful conclusion can be drawn by inspecting the contents of that box and then pointing out that if his daughter were to pick that box, she would get those contents. The truth is that the contents of box B are simply irrelevant. The father could leave it empty or he could put a stone in it. He could even put a million dollars in it! Indeed, it does not even matter whether box B exists at all. As mentioned previously, the father could simply hold the anklet behind his back, invite his daughter to make the choice, and then reveal the anklet when she chooses it, as he knows she will.
I guess this last case, in which the father is simply holding the anklet behind his back, makes everything particularly vivid. Am I really holding that, in this bare case too, the girl continues to have a choice between the anklet and the bracelet? I certainly am, for the reasons already given. Given that the father fully intends to offer her that choice, then the only thing (in our story) that could rob her of it is his failure to procure the bracelet. But I have already explained why this failure on his part is entirely principled and deserving of no censure. And so that failure in itself cannot be said to have robbed her of the choice in question. So I see no grounds to think that she has been robbed of the choice at all.
Someone could of course just stand their ground and steadfastly require that both gifts be present before the girl may be said to have a choice between the two. To my mind, however, this requirement is just a prejudice of habit arising from the fact that the requirement would normally have to be in place. Normally, if you offer someone a choice between two items, you do not know which item they will choose, and so it matters for your offer to be sincere that both items be made available for their taking, in case either one is chosen. Likewise, it would normally be a “necessary condition,” for something to be among your choices, that you will get it if you choose it. (This is just another way of saying that the item must be available for your taking.) The case of the knowing father is not normal in this way however and—in my opinion—exposes the requirement for the unthinking prejudice that it is. To apply the requirement perfunctorily in such an unusual case is to fail to grasp why the requirement should normally be present at all.
I also believe that, in actual practice, this sort of issue would cause us little difficulty. It is only in theory that we allow ourselves to be befuddled!
Consider an airline that offers every passenger a choice between beef and chicken (say) as the main dish of their complimentary meal. From experience, the airline knows that its passengers are fairly predictable: about half of them will tend to choose beef; the other half chicken. So, on a typical flight with five hundred passengers on board, the airline knows that it doesn’t really need to prepare five hundred servings of beef and five hundred servings of chicken in advance! About three hundred servings of each will do: the extra fifty apiece sufficing to accommodate the vagaries of chance. Should we complain that this airline was depriving some of its passengers of a choice between beef and chicken? Specifically, that for each passenger to genuinely have the choice in question, the airline would really need to prepare five hundred servings of beef and five hundred servings of chicken in advance? If the airline had no idea what its passengers would choose, yet prided itself on its ability to offer every passenger the choice in question, the complaint might have some merit. But if the airline knows that its passengers tend to split evenly between the two, the charge seems to me perverse.
This example is statistical in nature but the underlying point is the same. Given that the airline knows what its passengers will tend to choose, it is not really necessary to set aside one serving of beef and one serving of chicken per passenger in order that everyone may be said to have a genuine choice between the two. Indeed, I dare say that any airline consultant who believed that this was necessary would be fired on the spot! But this is what you must believe if you believed in the same way that the father really has to bring both gifts to the table in order that his daughter may be said to have a genuine choice between them, notwithstanding that he already knows which gift she will choose. It is exactly the same issue.
The statistical example is useful because we are familiar in practice with the law of large numbers. Our imaginations are not stretched by the thought that an airline knows what large numbers of its passengers will tend to do, or that a shoe manufacturer knows which models its myriad customers will tend to buy, etc. In contrast, it is considerably more difficult to reliably predict the behaviour of a single person, as in a father who claims to know which gift his daughter will choose. We cannot so easily draw on everyday experience when it comes to a case of this sort. But this should not stop us from drawing the right conclusion anyway because the case is stipulated to be one in which the father does have such knowledge. Of course, as mentioned above, if you think that such foreknowledge is impossible, then it is open to you to reject the hypothetical scenario entirely. Otherwise I believe that it may be just a failure of logical nerve to resist the conclusion I am recommending, viz., that the knowing father does not rob his daughter of the choice between the anklet and the bracelet by neglecting to procure the bracelet.
I won’t belabour my position any further since the essential points have been made and anything else I say would just be rhetorical and repetitive!
It may be useful however to situate the position I am recommending with reference to the “compatibilist” assumption mentioned a while back. This is the assumption that foreknowledge of choice is compatible with freedom of choice. I took this assumption for granted in my story of the father and the daughter and pointed out that it is widely granted in the context of Newcomb’s problem as well. (I fully accept the assumption myself.) Compatibilism says that if I offer you a choice between A and B, you are not robbed of that choice just because I know you will choose A. Very well, and I am merely pushing this idea one small step further. You are also not robbed of that choice if I fail to make B available for your taking if the reason for this is that I know you will choose A.
If you accept the basic compatibilist position, then you should really accept the extension as well, because it really is quite natural. I take this to be the essential lesson of the father and the daughter. Incidentally, when Martin Gardner first encountered Newcomb’s problem, he was reminded of William James’s remark that not all of the juice may have been pressed out of the free-will controversy. Given what I just said, I cannot help but agree. There’s some extra juice that we can get out of it, as just explained.
6. Newcomb’s problem
How does all of this bear upon Newcomb’s problem? The broad idea may already be clear but I should make the details explicit. The lesson of father and daughter contains the seeds of a certain solution to Newcomb’s problem which I find completely satisfying and will now explain using the more natural variant of the problem shown above. To remind you:
You may take box A or box B. If the man foresaw that you would take box A, he has placed you in this situation:
while if he foresaw that you would take box B, he has placed you in this one:
Which box should you take?
I pointed out that a traditional one-boxer will take box B whereas a traditional two-boxer will take box A. My own instincts are indeed to take box B but I wanted also to do this “in good conscience,” i.e., in full knowledge that box A contains more money! So I needed a satisfying way of seeing what was wrong with the simple and suasive argument for taking box A, which is essentially this: “In either situation, box A contains more money than box B. So, whichever situation is yours, you should take box A!”
I can now say that the essential mistake in this simple and suasive argument is to think that, in choosing between box A and box B, you are choosing between the actual contents of those boxes!
This is the same mistake we saw above in the case where the father places a stone in box B just for weight. In that case, I explained why it was a mistake to think that, in choosing between box A and box B, the girl was choosing between an anklet and a stone. Since the father knew that she would not choose box B, he was free to put whatever he liked in it, and so its contents are simply irrelevant. In particular, we should not treat those contents—the stone—as being among the girl’s choices. Rather, in choosing between box A and box B, the girl is continuing to choose between an anklet and a bracelet. The stone doesn’t come into it at all.
Newcomb’s predictor is exactly like the knowing father in this respect. Since he knows which box you will choose, the contents of the other box become irrelevant. He can put anything he likes in the box he knows you will not choose and it won’t mean a thing. So, in deciding whether to take box A or box B, you mustn’t try to compare their actual contents. This serves no purpose because while the contents of the one box is relevant, the contents of the other is not.
Put another way, you must not assume that your choice between the two boxes “boils down” to a choice between their actual contents. But this is exactly what the simple and suasive argument above assumes. It compares the contents of both boxes, notes that box A contains more money than box B, and so recommends taking box A. The mistake is easy to miss but, once we are clear about the lesson of the father and daughter, it is not difficult to spot. It is true that box A contains more money than box B, and it is (thereby) also true that you will get more money if you take box A than if you take box B. We may concede these things. But it doesn’t follow that you should take box A. In choosing between the predictor’s boxes, you are not choosing between their actual contents, any more than in choosing between the father’s boxes, the girl was choosing between an anklet and a stone.
What then are you choosing between, in choosing between box A and box B? Given everything I have said, the answer is forced upon us: you are choosing between a thousand dollars and a million. We can make this clear by identifying the “irrelevant” amounts in the boxes and replacing them (for the moment) with stones. We then get the following case, which is not quite Newcomb’s problem, but a useful intermediary:
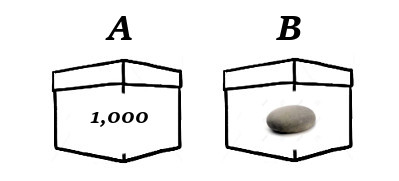
As before, you may take either box, but if the man foresaw that you would take box A, he has placed you in this situation:
while if he foresaw that you would take box B, then he has placed you in this one:
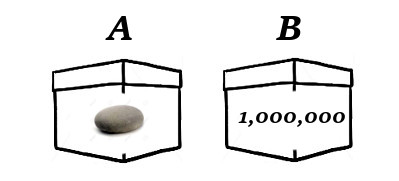
Note the presence of the stones. In the first situation, box B contains a stone, whereas, in the second, box A does. These are the boxes that, in the respective situations, the man knows you will not pick and the stones are a vivid way of registering that their contents “don’t matter.” The man can place anything he likes in these boxes, but let these be stones for now, to fix the idea.
Suppose that the man now claims, in this curious way, to be offering you a choice between a thousand dollars and a million. What should we make of this? If you accept that he knows which box you will take, can you regard yourself as having the choice in question?
No doubt, the “natural” reaction is that the man’s offer is nonsensical and that no such choice is before you. For if he has placed you in the first situation, then, in choosing between box A and box B, you are essentially choosing between a thousand dollars and a stone, whereas if he has placed you in the second, you are essentially choosing between a stone and a million dollars. In neither case, do you have a choice between a thousand dollars and a million!
I hope it is clear why I think this “natural” reaction is mistaken. In my opinion, this is a perfectly legitimate (though unusual) way for someone to offer you a choice between a thousand dollars and a million. Specifically, your choice is between the thousand dollars in box A in the first situation, and the million dollars in box B in the second. This may sound nonsensical since you cannot be in both situations at the same time. The rejoinder is that you don’t have to be, in order for the choice in question to be yours. After all, you cannot choose both amounts at the same time either, and so the man can take advantage of this fact.—The amount it is known you will not choose doesn’t actually have to be placed before you.
It would be exactly the same if the father were to bring these boxes to the table if he foresaw that his daughter would choose the anklet:
but these boxes if he foresaw instead that she would choose the bracelet:
Here, the “irrelevant” boxes have been left empty instead of being filled with stones. This makes no difference of course. Given the father’s precognitive powers, this would likewise be a legitimate way of offering his daughter the choice between the anklet and the bracelet.
7. Putting everything together
Once we see this, it is a short step to making sense of what is really going on in Newcomb’s problem. Or perhaps what might be going on, because I’m about to “redescribe” the predictor in a way that goes slightly beyond tradition in order to accommodate what I have said so far. This will be okay because the logical structure of Newcomb’s problem will remain untouched.
Imagine that the predictor actually wants to offer you a choice between a thousand dollars and a million, but plans to do this in such an unusual way that you may end up disbelieving that the choice has been offered to you. (E.g., half of the people to whom the alleged choice is offered reckon that no such choice has been offered to them at all.) The predictor proceeds exactly as before, without the stones:
You may take box A or box B. If he foresaw that you would take box A, then he has placed you in this situation:
while if he foresaw that you would take box B, then he has placed you in this one:
Which box should you take?
As mentioned, two reactions are possible. The first is to accept that this is a perfectly legitimate (though unusual) way for the man to offer you a choice between a thousand dollars and a million. If you react in this way, then you will accept that, in choosing between box A and box B, you are indeed choosing between these amounts, and so you will simply take box B and pocket the million. You will not be distracted by the boxes that essentially contain “stones”—the top-right and bottom-left boxes in the diagrams above. These boxes contain 0 and 1,001,000, respectively, but the predictor could have placed just about anything in them without affecting your decision to take box B.
What is the significance of the amounts 0 and 1,001,000? Why did the predictor put those amounts in the “irrelevant” boxes? The answer has to do with the second reaction you might have towards this unusual situation, which is to reject any suggestion that a choice between a thousand dollars and a million is before you. We have already seen why someone might react in this way and I don’t think I need to repeat the explanation here, but we do need to consider what such a person would do if they did react in this way. Which box would they take?
This is the “complication” mentioned above of the daughter who somehow discovers that her father has left one of the boxes empty and objects thereby to the suggestion that the choice between the anklet and the bracelet is really before her. I suppressed this possibility at the time because it would have introduced unnecessary complications into her reaction and behaviour that the father might have been unable to predict. We cannot avoid these complications now since the modus operandi of the predictor is in the open.
And so, which box will you take if you reject the suggestion that a choice between a thousand dollars and a million is before you? The answer of course is that you will take box A, on the “natural” grounds that, whichever situation you are in, box A contains more money than box B. This is the significance of the amounts 0 and 1,001,000 above: they are designed to ensure that box A always contains more money. Notice that, if the predictor had used stones instead, you would no longer have reason to take box A. This is why the version involving stones does not generate Newcomb’s problem in the same way.
This means also that, in order to predict which box you will take, the predictor simply has to anticipate whether you will accept or reject the suggestion that a choice between a thousand dollars and a million has been laid before you.—This, we may suppose, is essentially what the predictor is good at anticipating. We need to put the matter this way because the alternative makes no sense. He cannot predict which box you will take by trying (instead) to anticipate whether you will choose the thousand dollars over the million, or the million dollars over the thousand. That makes no sense because, if you believed that you had that choice, you would of course favour the million. What the predictor is anticipating rather is whether you would believe that you had that choice. Once he foresees this, he can immediately infer whether you will take box A or box B—provided the right amounts are used as “stones.”
And so we have a way of understanding what is going on in Newcomb’s problem which coheres with my previous explanation of where the argument for taking box A goes wrong.
The way I see it, the question of whether you should take box A or box B just reduces to the question of whether someone can bestow upon you a choice between a thousand dollars and a million in this rather unusual way. I believe that the answer is “can” and that you should therefore take box B.
Those who reject this answer and favour taking box A will presumably also reject that the girl had the choice between the anklet and the bracelet in the birthday case above. Their view would be that, having neglected to procure the bracelet, her father has robbed her of the choice between the anklet and the bracelet, notwithstanding that he knew that she would not choose the bracelet. Although I think that this view is demonstrably incorrect—and I have tried my best to demonstrate this above—I do not think it is silly. After all, such a distinguished philosopher as David Lewis seems to have held it. These are his words, on behalf of two-boxers in Newcomb’s problem, or A-boxers in the variant above:
8. Concluding remarks
The analysis above might be supplemented in various ways but this essay is long enough already and there is also a danger (if I keep on babbling) of losing the forest for the trees.
So I won’t worry about explaining, for instance, how the analysis can be adapted to the traditional version of Newcomb’s problem, in which you must choose between both boxes and box B, rather than between box A and box B. This sort of detail—and others like it—can be filled in easily by anyone who has read this far.
I should say something however about my use of the word ‘know’ in connection with the predictor’s abilities. I have spoken freely of the predictor knowing which box you will take because this makes it easy to see how something can be among your choices even if it is not there for your taking. Thus, if he knows which box you will take, then it does not matter if he leaves the other box empty, or puts irrelevant stuff in it. This idea does not come across so naturally if the predictor is described in a more precised and nuanced way, e.g., as being likely to have correctly predicted which box you will take.
Nevertheless, the more nuanced way is how Newcomb’s predictor is traditionally described. The talk is in terms of probabilities because this allows us to characterize the predictor’s abilities in a considerably more general way. It also facilitates a mathematical treatment of the issue. So, for instance, the predictor might be said to be 90% accurate, or 60% accurate, or any number in between, and we can ask how varying this number affects the question of which box to take. In contrast, blunt talk of the predictor’s knowing (or not) which box you will take does not adequately address the various possibilities.
So it is fair to ask what happens to our analysis if we speak in terms of probabilities instead? Suppose that the predictor is 90% accurate, in the sense that 90% of one-boxers find him to have predicted their choice correctly, and likewise for two-boxers. (E.g., his track record shows this.) It is your turn to play. Can you continue to think of the choice between a thousand dollars and a million as being before you? Since the predictor sometimes errs, it is not straightforward to say that he knows which box you will take, which was my previous condition for the choice in question to be before you. But he is clearly not just guessing either, so it is not straightforward to say either that you have been robbed of the choice in question. How do we understand what is going on here?
It would take a whole other essay to address this issue properly, but I can easily sketch a meaningful approach here. Imagine facing a predictor who is 90% accurate. Is there a simple way to relate such a predictor to one who knows which box you will take?—If so, we can then avail ourselves of our previous analysis. Well, one way is as follows. Faced with such a predictor, just think of yourself as entering into a gamble in which there is a 90% chance that the predictor knows which box you will take, and a 10% chance that he has bungled it and gotten it wrong. (Other ways are possible but this one is quite simple.) Following our previous analysis, we can then say that there is a 90% chance that, in choosing between box A and box B, you are choosing between a thousand dollars and a million, and a 10% chance that you are choosing instead between whatever “stones” the predictor has placed in the irrelevant boxes. Given the values of the “stones,” we can then calculate which box is better to take. This would normally be done with a traditional expected-utility calculation, which is indeed how one-boxers typically justify their decision to take box B. And so we see that the analysis above is consistent with the traditional way of justifying the decision to take box B.
Two-boxers in Newcomb’s problem typically reject any such calculation because they think (at bottom) that there is no sense in which a choice between a thousand dollars and a million can be said to be before you, as such a calculation implicitly assumes. But once we see the error behind this way of thinking, the traditional calculation seems to me to emerge unscathed. I actually see nothing in Newcomb’s problem which calls traditional expected-utility reasoning into question.
I will leave this sketch there because I am not really concerned to defend the decision to take box B in this essay. To fully defend it would require a substantial excursion into that branch of mathematics and philosophy known as decision theory. I have been concerned rather to give a plain-language account of my struggle with the argument for taking both boxes. I began by saying that I have always been a one-boxer and that Newcomb’s problem (for me) has always been the problem of pinpointing the error in the simple and suasive argument for taking both boxes. Here is a quote from Howard Sobel—a well-known two-boxer—that throws down the gauntlet in exactly the right way:
References
– Jordan Howard Sobel, Puzzles for the Will
I cannot recall when I first heard of Newcomb’s problem but I do remember that the first time it gripped me I was immediately a one-boxer.
That is to say, I was a one-boxer from the start. One-boxing instinctively felt right to me—notwithstanding the evident force of the two-box argument.
This left me with the nagging problem of explaining what then was wrong with the simple and utterly suasive argument for taking both boxes. And this problem seemed to me so interesting that I was soon thinking about it day and night. For me, this has always been the real issue in Newcomb’s problem and what follows is largely an account of my battle with the argument for taking both boxes.
I assume that Newcomb’s problem is understood because I want to jump right in. Here’s a quick statement so that you can see that I’m indeed talking about the standard problem introduced by Robert Nozick in 1969. (“It is a beautiful problem. I wish it were mine.”)
Two boxes A and B are before you. You know that box A contains $1,000 whereas box B contains either a million dollars or nothing, though you don’t know which. You may take both boxes or just box B, where you will get whatever money is contained in the box or boxes you take. However, a man has predicted in advance (e.g., yesterday) which choice you would make and has left the million dollars in box B if he predicted that you would take just box B, as opposed to nothing in box B if he predicted that you would take both boxes. You have reason to believe that this man is very likely to have predicted your choice correctly, e.g., he has an excellent track record of such predictions. If your only aim is to get as much money as you can, should you take both boxes or just box B?This is Newcomb’s problem and it is a problem because, given the facts described, there is a very compelling argument for taking both boxes but an equally compelling argument for taking just box B. Again, I assume that these arguments are well-known—though more on this below.
I don’t think very much hangs on this however. My main reason for speaking of the predictor as knowing what you will do is that later I will describe a case involving a father who wishes to offer his daughter a choice between two gifts on her birthday but knows in advance which gift she will choose. This is meant to be an ordinary description of a sort of case with which we are all familiar—a case of “foreknowledge”—and it is perfectly natural to use the word ‘know’ in this sort of context. I will then compare this man to the predictor in Newcomb’s problem. So the predictor knows which choice you will make in the same sense that the man knows which gift his daughter will choose. Speaking in this ordinary way will make some of what I say below much easier to understand. (I will revisit this point at the end.)
Someone might question whether anyone could ever know what they were going to do in such a situation as Newcomb’s. If so, they can resolve Newcomb’s problem by pointing this out – no predictor could ever know what they were going to do any more than any father (say) could ever know what his daughter was going to do! The ensuing contradiction between the argument for taking both boxes and the argument for taking just box B can then be traced back to the “absurd” supposition that the predictor knew what they were going to do. I don’t know of anyone who thinks that this is a good way to resolve Newcomb’s problem though. There is a better way.
So how do we resolve Newcomb’s problem? I mentioned that I was a one-boxer from the start and that, for me, the real problem has always been to explain what was wrong with the simple and suasive argument for taking both boxes.
So I’m going to say very little about the case for taking just box B in what follows. I think that this case is basically sound. If you have every reason to believe that the predictor knows what you will do, then you have every reason to expect a million dollars if you take just box B as opposed to a mere $1,000 if you take both boxes. You thus have every reason to take just box B. This states the case in plain language. Were more precision required, a one-boxer could appeal to a traditional “expected-utility” calculation—a kind of mathematical calculation whose details I assume are familiar. I will say something about this towards the end, but bear in mind that I’m not really concerned with the one-box argument in this essay. I want rather to expose what I think is the flaw in the argument for taking both boxes. As I said, this is the story of my battle with the two-box argument.
Some people place little faith in philosophical instincts when it comes to these sorts of things, but I’m not one of them. I believe that one can often have a “nose” for the right way to go. In a game of chess, a player can often have a nose for whether to move his bishop or knight in a difficult position without being able to fully explain his decision. In philosophy, one can likewise have a nose for the right path to follow. My nose has always told me that something is wrong with the argument for taking both boxes, the question only being to pin it down. So let me turn to this argument at once.
2. The two-box argument
The case for taking both boxes can be made in many ways. People sometimes invoke technical apparatus like dominance reasoning or causal decision theory to show that it is better to take both boxes but I tend to find that plain language is sufficient. Newcomb’s problem has always gripped me in plain language and I have always sought to resolve the difficulty likewise. Thus, as the boxes stand before you, it is obvious that there is more money in both boxes than in box B alone. This cannot be reasonably denied. In fact, it cannot be denied at all. Regardless of what the man has predicted, regardless of how accurate he is, and regardless of what he has placed in box B, you know that there is more money in both boxes than in box B alone. Indeed, you know that there is exactly a thousand dollars more. It follows that you will get more money (a thousand dollars more) by taking both boxes than by taking box B alone. Since money is your aim, you must accordingly do so.
This simple argument bothered me so much that I dropped everything and started thinking about it day and night.
I felt that something had to be wrong with it but for the life of me couldn’t see what. You can pick at the argument in various obvious ways but it’s not easy to find anything convincing to say against it. And I wanted something convincing, something you could feel in your bones.
Consider for example the “fly in the ointment” mentioned above – your belief that the predictor knew which choice you would make. The most glaring thing about the two-box argument is that it ignores this aspect of the problem completely. The predictor does not even get a mention! This is most disconcerting. Surely this is the error in the two-box argument, viz., that it ignores a feature of the problem—the predictor’s powers—that is obviously relevant to your eventual decision?
This is a natural objection to make and essentially the first one that anyone thinks of. But you don’t have to look very far to see that it is not (ultimately) very convincing. It is true that the two-boxer ignores a feature of the problem that seems to be relevant, viz., the powers of the predictor. But a similar charge can be levelled against the one-boxer! What the one-boxer ignores is the plain fact that, as the boxes stand before him, there is more money in both boxes than in box B alone. This feature of the problem also seems to be relevant to your eventual decision. And the one-boxer doesn’t even mention it! So this is a case of the pot calling the kettle black – not very convincing.
The truth is that Newcomb’s problem contains two prominent features, both of which seem to be relevant, but which pull curiously in opposite directions. To have a balanced view of the problem, we must be sensitive to both features. If you focus on the powers of the predictor, then it can easily seem that taking box B alone is better. (Given his powers, you will get a million dollars if you take box B alone but just $1,000 if you take both boxes.) But if you focus on the fact that—as the boxes stand before you—there is more money in both boxes than in box B alone, then it can easily seem that taking both boxes is better. (If there is more money in both boxes, then you will get more money if you take both boxes.) Are we to say that one of these features is more relevant to your decision than the other? But which one and why? Offhand, there seems to be no saying.
Before explaining how I think this can be done—and how the resulting picture reveals (in my opinion) where the two-box argument really goes wrong—let me explain how another philosopher thought this could be done. This other philosopher was David Lewis. Unlike me, Lewis was a two-boxer and felt that there was nothing wrong with the two-box argument at all. So his overall picture of things is going to be very different from mine. But this doesn’t matter for now: the important thing is to appreciate how it is possible to think about Newcomb’s problem in such a way that both of the aforementioned features of the problem are accommodated at once.
As mentioned, Lewis believed that it was better to take both boxes than to take box B alone. He believed that you would get more money by doing so, i.e., because there is more money in both boxes. This accommodates the one feature of our problem. But Lewis did not ignore the powers of the predictor either. To accommodate them, he attempted to “make sense” of the fact that one-boxers in this game tend to end up with more money than two-boxers. Note that this fact is not in dispute and is essentially built into the problem. (If the fact did not hold, the predictor’s powers would be in question, and they are not supposed to be in question.) But Lewis did not think that the fact showed that one-boxing was the right thing to do. He interpreted it as showing rather that the predictor was (for some reason) rewarding irrational people!
This sounds like a joke at first, but only at first. To see Lewis’s point, it helps to imagine a case where it is clear that the predictor is rewarding irrational people. It helps to see that such a thing is possible and that Lewis was not simply grasping at straws. So imagine a predictor who can tell in advance whether someone is rational or irrational. Whenever he meets a rational person, he presents her with two open boxes A and B, where A contains $1,000 and B contains nothing. The amounts in the boxes are plain to see and the subject is invited to take either both boxes or box B alone. Being rational, she naturally takes both boxes on the (correct) grounds that she gets more money that way. Irrational people are likewise presented with two open boxes A and B, but this time A contains $1,000 and B contains a million dollars. They too may take either both boxes or just box B and the amounts in the boxes are again plain to see. Being irrational, they take just box B on the (silly) grounds that they get less money that way. Note that, in either case, taking both boxes is the rational thing to do; it is just that irrational people fail to see this. Nevertheless, they end up with a million dollars whereas rational people get just $1,000. In this case, it seems clear that the predictor is (for some reason) rewarding irrational people.
Lewis believed that something like this was going on in Newcomb’s problem, except of course in a more subtle way. He recommended this view in a short paper in 1981, after the suggestion was first made by the philosophers Gibbard & Harper in a longer and more technical paper in 1978. The upshot was that two-boxers could now take both boxes “in good conscience,” as it were. For here was a way of embracing the predictor’s powers while maintaining that taking both boxes was the rational thing to do. It should be emphasized, as Lewis himself did, that none of this shows that taking both boxes is the rational thing to do in Newcomb’s problem and that taking just box B is irrational. The point is only that the two-boxing position is overall coherent: it can accommodate all the relevant features of the problem. In particular, the objection that the two-boxer ignores the powers of the predictor is now completely defanged. So if you are independently persuaded that taking both boxes is the right thing to do, this way of looking at the matter can be recommended.
Not me, however. I was independently persuaded that taking just box B was correct. So I had the opposite problem from Lewis, Gibbard and Harper. I needed a way of looking at things that accommodated the fact that there was obviously more money in both boxes than in box B alone. How does a one-boxer take just box B in the face of this fact?
After thinking for a considerable time—many months, if the truth be told—the answer finally came to me. Not only did I understand how to one-box “in good conscience,” I also understood what was wrong with the argument for taking both boxes.
3. A more natural variant
To explain this, it helps to consider a simple variant of Newcomb’s problem. Traditionally, your choices are between taking both boxes and box B alone – an honoured tradition I have observed so far. But this way of putting it can be a little confusing. It is more natural to have a choice between taking the one box or the other. It is not hard to set this up, so let’s do it. This is what I did in the course of things and it helped me see what was wrong with the two-box argument.
In this variant, there are still two boxes A and B, but your choices are simply between taking box A (alone) and taking box B (alone). This is slightly more natural. And now, if the man predicted that you would take box A, then he has (already) placed $1,000 in A and nothing in B. Like this:
On the other hand, if he predicted that you would take box B, then he has (already) placed a million-and-a-thousand dollars in A and a million dollars in B. Like this:
One of these situations is yours but you have no idea which one. (The boxes are opaque.) Note that box B contains either nothing or a million dollars and, in either case, box A contains a thousand dollars more. You may take either box A or box B in the knowledge of the facts just stated and the belief that the man knew which box you would take. Which box should you take?
A traditional one-boxer would take box B whereas a traditional two-boxer would take box A. (I hope this is obvious.) And my instincts indeed tell me that I should take box B. (“If the predictor knew what I would do, then if I take box B, he will have placed me in the second situation and I will get a million, whereas if I take box A, he will have placed me in the first and I will get just $1,000.”) But it is hard to ignore the simple case for taking box A, which is that, in either situation, box A contains more money than box B. So, no matter which situation the man has placed me in, I should take box A!
In terms of this variant, my goal is to explain how someone can sensibly (“in good conscience”) take box B despite knowing that box A contains more money! As it turns out, the explanation will also show where the argument for taking box A goes wrong. Everything I say below can easily be adapted to the traditional version of Newcomb’s problem.
4. Father and daughter
Suppose that the gifts in question are an anklet (A) and a bracelet (B): the father is letting his daughter choose one of these as a birthday gift. For our purposes, imagine that the father presents his daughter with two gift-wrapped boxes, e.g., as pictured above. (He has purchased both gifts in advance and has wrapped each in a box of its own.) The boxes are labelled A and B, with the obvious meanings, and the daughter is invited to choose between the anklet and the bracelet by picking the appropriately-labelled box.
In an ordinary case, the girl would just make her choice—the anklet, say—and pick the appropriate box: A, in this case. The father would then have to “dispose” of the gift she did not choose—the bracelet—e.g., by sending it back to the store for a refund.
But suppose that the father knows in advance that his daughter will choose the anklet over the bracelet – a case of “foreknowledge.” How does the father know this? Well, we can just suppose that he knows his daughter well. (We needn’t suppose that she told him as much.) Here’s the question that I really want to pursue: in this case, does the father really need to procure the bracelet in advance and place it in box B? He knows, we are supposing, that his daughter is not going to pick the bracelet, so it seems fair to ask why he should trouble himself to purchase it knowing that he will eventually have to return it to the store for a refund? There is a case here for saying that he doesn’t really need to get the bracelet in advance. He does need to get the anklet and place it in box A, of course, since he knows that his daughter is going to choose it. But I don’t see that he needs also to get the bracelet to be able to sincerely offer her a choice between the anklet and the bracelet on the day in question.—At least, this is what I plan now to argue.
Let me make things clear before proceeding. Here is a girl, presented with two opaque boxes A and B. Her father offers her a choice between an anklet and a bracelet and invites her to pick the appropriately-labelled box. She thinks for a while and then picks box A, just as her father knew she would. She thereby gets an anklet. Unknown to her, box B is empty. It does not contain a bracelet because her father reasoned that, since he knew that she was not going to choose the bracelet over the anklet, he need not bother getting it. The father then simply disposes of the empty box B, glad to have saved himself the trouble of returning to the store a bracelet that he knew she was not going to pick. And the question I’m asking is this: did the girl really have a choice between an anklet and a bracelet in the situation as described? In particular, did her father deprive her of that choice by failing to procure the bracelet?
I’m going to try to persuade you that the answer to the last question is no. Notwithstanding that no bracelet is anywhere in the vicinity, and we may even imagine that all bracelets have been sold out by now, and even that the father foresaw that this would be so, he did not deprive his daughter of the choice in question by failing to procure the bracelet, i.e., by leaving box B empty. This is essentially because he knew that she would not choose the bracelet anyway.
Before trying to persuade you of this, let me address three questions that sometimes arise when I bring this example up with friends.
Well, let me first say that the rigamarole will eventually help me compare the situation with Newcomb’s problem, with its two boxes and so on.—But never mind this for now, because we can also answer the question on its own terms. Suppose that the father wants his daughter to make the choice anyway because he believes that she will value the gift more if it is of her own choosing (say). Lots of people believe some such thing and the father could easily be one of them. Or we could tell a longer story. Suppose that it is a hallowed tradition in this family that every daughter on her sixteenth birthday shall be given a choice between an anklet and a bracelet and it is the youngest daughter’s turn. The father is bound to tradition and so must present the choice to his daughter notwithstanding that he already knows which gift she will choose. So there are any number of reasons why the rigamarole might be necessary, apart from my desire to connect the case with Newcomb’s problem. Note also that I’m assuming that you can meaningfully ask someone to choose between two options even though you already know which option they will choose. This is the familiar philosophical assumption that foreknowledge of choice is compatible with freedom of choice. This assumption is widely accepted and I won’t feel the need to defend it here, especially since the assumption is also made in the context of Newcomb’s predictor and usually allowed without question. (The predictor knows what you will do, but you have a free choice in the matter anyway.) I will say a little more about this “compatibilism” below.
Second, one can wonder whether the father needs to bother with two boxes if he is going to leave one of them empty. If he has decided not to procure the bracelet (on the grounds explained above), then why bother with the second box at all, which shall after all simply remain empty? Why not just present his daughter with one gift-wrapped box, containing the anklet, and invite her to choose between the anklet and the bracelet before opening the box? Or why not just hold the anklet behind his back, invite her to make the choice between the anklet and the bracelet, and then present her with the anklet when she chooses it, as he knows she will. The answer is that either of these alternatives is (ultimately) also acceptable. In either of these cases too, I would say that the father does not deprive his daughter of the choice between the anklet and the bracelet, as will be clear from my discussion below. Again, I’m telling the story with two boxes mainly because it makes the comparison with Newcomb’s problem easier.
Finally, one might ask if it makes a difference if the daughter were to realize that one of the boxes before her was empty. The way I’m telling the story, the father leaves one of the boxes empty without alerting his daughter to this fact. Suppose however that the daughter (somehow) catches on to what her father has done. So she knows that, while one of the two boxes before her contains the gift her father is expecting her to choose, the other box is simply empty. And yet she is being asked to “choose” between the two gifts. Will she not vehemently protest that no such choice is before her and that she has no choice but to take the gift her father has bought, since the other gift is not available for her taking? Well, this is exactly the question I wish to pursue so we can turn to this at once. For the purposes of the story, it helps if the daughter is not made aware of the situation since this introduces unnecessary complications concerning her reaction and behaviour that are not relevant to the point I wish to make. I will revisit these complications when I compare the father to Newcomb’s predictor as they will be more relevant then. For the moment, let us assume that the daughter does not realize that one of the boxes before her is empty.
5. A question of choice
And so—finally—does the daughter really have a choice between an anklet and a bracelet in the situation as described? In particular, has the father robbed her of that choice by procuring just the anklet—the gift he knows she will choose—while deliberately neglecting to procure the bracelet?
From my experience, a natural first reaction is that the father has indeed robbed his daughter of the choice in question by his somewhat cavalier behaviour. One thinks: for the choice between the anklet and the bracelet to be genuinely before her, both gifts must be available for her taking. But the father has made one of them (the bracelet) unavailable, thereby robbing her of the choice between the two. And so, whether she realizes it or not, the girl really has no choice but to take the only gift that her father has procured—the anklet, as we are supposing. The choice of the bracelet is not really before her!
I said above that I hold the opposite view, and so I think that this natural reaction is mistaken. But let me first mention a slightly different case for which I think such a reaction would be appropriate. Suppose that the father doesn’t really know which gift his daughter will choose but decides for some reason to guess. He guesses that she will choose the anklet (say) and decides bravely to purchase it alone. The rest of the story is then as before: he presents her with two boxes A and B, where A contains the anklet and B is empty. The daughter chooses box A and is pleased to receive the anklet. And the father simply throws away the empty box B. In this case, I’d be the first to agree that the father did rob his daughter of the choice between the anklet and the bracelet. Notwithstanding that the girl goes away pleased, she had no real choice but to take the anklet and the father was just lucky to get away with it.
This case of course is not the same as ours. In our case, the father doesn’t just guess that his daughter will choose the anklet but knows that she will do so. Does this make a difference? I think that it does: that the girl ends up choosing the anklet—the only gift her father has brought to the table—is now no longer a matter of luck. We cannot now rail that the father was “lucky to get away with it.” Luck is no longer at issue because he knew that she would not choose the bracelet. As such, his failure to procure the bracelet can no longer be grounds for censure. Or so it seems to me! I find it useful to put the matter in this way, in terms of whether the father’s failure to procure the bracelet occasions any censure—because it is easier to have an opinion on this question. Moreover, if we agree that it does not, then I think we should agree that his daughter was not for that reason deprived of the choice between the anklet and the bracelet. But there is no other reason (in our story) why she should have been so deprived. This is what satisfies me that she has not been deprived of the choice in question at all. In this sense, the choice between the anklet and the bracelet remains open to her despite the fact that the bracelet is not available for her taking.
This states the essential case, but I guess I should say a little more since everything is going to hang on this before long!
In the case described, where the father neglects to procure the bracelet in the knowledge that his daughter will choose the anklet, there is perhaps an obvious underlying worry. This concerns what would happen were his daughter to choose the bracelet. The father knows that she will not but we can still ask what would happen if she did? Given that no bracelet is available for her taking, it is clear what the answer must be. Were she to choose the bracelet, she would not get it! (She would pick box B and find it to be empty.) But how then can the choice of the bracelet be said to be before her? Surely a necessary condition for something to be among your choices is that you will get it if you choose it?
The answer to this worry is not hard to see. If the father knows that his daughter will not choose the bracelet, then it is no longer appropriate to draw any conclusions by considering what would happen were she to do so. What would happen becomes irrelevant because the father can “set things up” in any way he likes, safe in the knowledge that she will not choose the bracelet. For instance, suppose that, instead of leaving box B empty, he places a stone in it, just for weight. Does this mean that, in choosing between box A and box B, his daughter is choosing between an anklet and a stone? After all, if she were to pick box A, she would receive an anklet, but if she were to pick box B, she would receive a stone! So, in choosing between the boxes, she must really be choosing between an anklet and a stone—whether she knows this or not! It seems to me however that only a superficial thinker would draw this conclusion. Once we understand that the contents of box B are up to the father, and that he knows that his daughter will not pick that box, it becomes clear that it means nothing to consider what would happen if she were to pick it. For, as I said, the father can put anything he likes in box B, safe in the knowledge that she will not choose it. So no meaningful conclusion can be drawn by inspecting the contents of that box and then pointing out that if his daughter were to pick that box, she would get those contents. The truth is that the contents of box B are simply irrelevant. The father could leave it empty or he could put a stone in it. He could even put a million dollars in it! Indeed, it does not even matter whether box B exists at all. As mentioned previously, the father could simply hold the anklet behind his back, invite his daughter to make the choice, and then reveal the anklet when she chooses it, as he knows she will.
I guess this last case, in which the father is simply holding the anklet behind his back, makes everything particularly vivid. Am I really holding that, in this bare case too, the girl continues to have a choice between the anklet and the bracelet? I certainly am, for the reasons already given. Given that the father fully intends to offer her that choice, then the only thing (in our story) that could rob her of it is his failure to procure the bracelet. But I have already explained why this failure on his part is entirely principled and deserving of no censure. And so that failure in itself cannot be said to have robbed her of the choice in question. So I see no grounds to think that she has been robbed of the choice at all.
Someone could of course just stand their ground and steadfastly require that both gifts be present before the girl may be said to have a choice between the two. To my mind, however, this requirement is just a prejudice of habit arising from the fact that the requirement would normally have to be in place. Normally, if you offer someone a choice between two items, you do not know which item they will choose, and so it matters for your offer to be sincere that both items be made available for their taking, in case either one is chosen. Likewise, it would normally be a “necessary condition,” for something to be among your choices, that you will get it if you choose it. (This is just another way of saying that the item must be available for your taking.) The case of the knowing father is not normal in this way however and—in my opinion—exposes the requirement for the unthinking prejudice that it is. To apply the requirement perfunctorily in such an unusual case is to fail to grasp why the requirement should normally be present at all.
I also believe that, in actual practice, this sort of issue would cause us little difficulty. It is only in theory that we allow ourselves to be befuddled!
Consider an airline that offers every passenger a choice between beef and chicken (say) as the main dish of their complimentary meal. From experience, the airline knows that its passengers are fairly predictable: about half of them will tend to choose beef; the other half chicken. So, on a typical flight with five hundred passengers on board, the airline knows that it doesn’t really need to prepare five hundred servings of beef and five hundred servings of chicken in advance! About three hundred servings of each will do: the extra fifty apiece sufficing to accommodate the vagaries of chance. Should we complain that this airline was depriving some of its passengers of a choice between beef and chicken? Specifically, that for each passenger to genuinely have the choice in question, the airline would really need to prepare five hundred servings of beef and five hundred servings of chicken in advance? If the airline had no idea what its passengers would choose, yet prided itself on its ability to offer every passenger the choice in question, the complaint might have some merit. But if the airline knows that its passengers tend to split evenly between the two, the charge seems to me perverse.
This example is statistical in nature but the underlying point is the same. Given that the airline knows what its passengers will tend to choose, it is not really necessary to set aside one serving of beef and one serving of chicken per passenger in order that everyone may be said to have a genuine choice between the two. Indeed, I dare say that any airline consultant who believed that this was necessary would be fired on the spot! But this is what you must believe if you believed in the same way that the father really has to bring both gifts to the table in order that his daughter may be said to have a genuine choice between them, notwithstanding that he already knows which gift she will choose. It is exactly the same issue.
The statistical example is useful because we are familiar in practice with the law of large numbers. Our imaginations are not stretched by the thought that an airline knows what large numbers of its passengers will tend to do, or that a shoe manufacturer knows which models its myriad customers will tend to buy, etc. In contrast, it is considerably more difficult to reliably predict the behaviour of a single person, as in a father who claims to know which gift his daughter will choose. We cannot so easily draw on everyday experience when it comes to a case of this sort. But this should not stop us from drawing the right conclusion anyway because the case is stipulated to be one in which the father does have such knowledge. Of course, as mentioned above, if you think that such foreknowledge is impossible, then it is open to you to reject the hypothetical scenario entirely. Otherwise I believe that it may be just a failure of logical nerve to resist the conclusion I am recommending, viz., that the knowing father does not rob his daughter of the choice between the anklet and the bracelet by neglecting to procure the bracelet.
It may be useful however to situate the position I am recommending with reference to the “compatibilist” assumption mentioned a while back. This is the assumption that foreknowledge of choice is compatible with freedom of choice. I took this assumption for granted in my story of the father and the daughter and pointed out that it is widely granted in the context of Newcomb’s problem as well. (I fully accept the assumption myself.) Compatibilism says that if I offer you a choice between A and B, you are not robbed of that choice just because I know you will choose A. Very well, and I am merely pushing this idea one small step further. You are also not robbed of that choice if I fail to make B available for your taking if the reason for this is that I know you will choose A.
If you accept the basic compatibilist position, then you should really accept the extension as well, because it really is quite natural. I take this to be the essential lesson of the father and the daughter. Incidentally, when Martin Gardner first encountered Newcomb’s problem, he was reminded of William James’s remark that not all of the juice may have been pressed out of the free-will controversy. Given what I just said, I cannot help but agree. There’s some extra juice that we can get out of it, as just explained.
6. Newcomb’s problem
How does all of this bear upon Newcomb’s problem? The broad idea may already be clear but I should make the details explicit. The lesson of father and daughter contains the seeds of a certain solution to Newcomb’s problem which I find completely satisfying and will now explain using the more natural variant of the problem shown above. To remind you:
You may take box A or box B. If the man foresaw that you would take box A, he has placed you in this situation:
while if he foresaw that you would take box B, he has placed you in this one:
Which box should you take?
I pointed out that a traditional one-boxer will take box B whereas a traditional two-boxer will take box A. My own instincts are indeed to take box B but I wanted also to do this “in good conscience,” i.e., in full knowledge that box A contains more money! So I needed a satisfying way of seeing what was wrong with the simple and suasive argument for taking box A, which is essentially this: “In either situation, box A contains more money than box B. So, whichever situation is yours, you should take box A!”
I can now say that the essential mistake in this simple and suasive argument is to think that, in choosing between box A and box B, you are choosing between the actual contents of those boxes!
This is the same mistake we saw above in the case where the father places a stone in box B just for weight. In that case, I explained why it was a mistake to think that, in choosing between box A and box B, the girl was choosing between an anklet and a stone. Since the father knew that she would not choose box B, he was free to put whatever he liked in it, and so its contents are simply irrelevant. In particular, we should not treat those contents—the stone—as being among the girl’s choices. Rather, in choosing between box A and box B, the girl is continuing to choose between an anklet and a bracelet. The stone doesn’t come into it at all.
Newcomb’s predictor is exactly like the knowing father in this respect. Since he knows which box you will choose, the contents of the other box become irrelevant. He can put anything he likes in the box he knows you will not choose and it won’t mean a thing. So, in deciding whether to take box A or box B, you mustn’t try to compare their actual contents. This serves no purpose because while the contents of the one box is relevant, the contents of the other is not.
Put another way, you must not assume that your choice between the two boxes “boils down” to a choice between their actual contents. But this is exactly what the simple and suasive argument above assumes. It compares the contents of both boxes, notes that box A contains more money than box B, and so recommends taking box A. The mistake is easy to miss but, once we are clear about the lesson of the father and daughter, it is not difficult to spot. It is true that box A contains more money than box B, and it is (thereby) also true that you will get more money if you take box A than if you take box B. We may concede these things. But it doesn’t follow that you should take box A. In choosing between the predictor’s boxes, you are not choosing between their actual contents, any more than in choosing between the father’s boxes, the girl was choosing between an anklet and a stone.
What then are you choosing between, in choosing between box A and box B? Given everything I have said, the answer is forced upon us: you are choosing between a thousand dollars and a million. We can make this clear by identifying the “irrelevant” amounts in the boxes and replacing them (for the moment) with stones. We then get the following case, which is not quite Newcomb’s problem, but a useful intermediary:
As before, you may take either box, but if the man foresaw that you would take box A, he has placed you in this situation:
while if he foresaw that you would take box B, then he has placed you in this one:
Note the presence of the stones. In the first situation, box B contains a stone, whereas, in the second, box A does. These are the boxes that, in the respective situations, the man knows you will not pick and the stones are a vivid way of registering that their contents “don’t matter.” The man can place anything he likes in these boxes, but let these be stones for now, to fix the idea.
Suppose that the man now claims, in this curious way, to be offering you a choice between a thousand dollars and a million. What should we make of this? If you accept that he knows which box you will take, can you regard yourself as having the choice in question?
No doubt, the “natural” reaction is that the man’s offer is nonsensical and that no such choice is before you. For if he has placed you in the first situation, then, in choosing between box A and box B, you are essentially choosing between a thousand dollars and a stone, whereas if he has placed you in the second, you are essentially choosing between a stone and a million dollars. In neither case, do you have a choice between a thousand dollars and a million!
I hope it is clear why I think this “natural” reaction is mistaken. In my opinion, this is a perfectly legitimate (though unusual) way for someone to offer you a choice between a thousand dollars and a million. Specifically, your choice is between the thousand dollars in box A in the first situation, and the million dollars in box B in the second. This may sound nonsensical since you cannot be in both situations at the same time. The rejoinder is that you don’t have to be, in order for the choice in question to be yours. After all, you cannot choose both amounts at the same time either, and so the man can take advantage of this fact.—The amount it is known you will not choose doesn’t actually have to be placed before you.
It would be exactly the same if the father were to bring these boxes to the table if he foresaw that his daughter would choose the anklet:
but these boxes if he foresaw instead that she would choose the bracelet:
Here, the “irrelevant” boxes have been left empty instead of being filled with stones. This makes no difference of course. Given the father’s precognitive powers, this would likewise be a legitimate way of offering his daughter the choice between the anklet and the bracelet.
7. Putting everything together
Once we see this, it is a short step to making sense of what is really going on in Newcomb’s problem. Or perhaps what might be going on, because I’m about to “redescribe” the predictor in a way that goes slightly beyond tradition in order to accommodate what I have said so far. This will be okay because the logical structure of Newcomb’s problem will remain untouched.
Imagine that the predictor actually wants to offer you a choice between a thousand dollars and a million, but plans to do this in such an unusual way that you may end up disbelieving that the choice has been offered to you. (E.g., half of the people to whom the alleged choice is offered reckon that no such choice has been offered to them at all.) The predictor proceeds exactly as before, without the stones:
You may take box A or box B. If he foresaw that you would take box A, then he has placed you in this situation:
while if he foresaw that you would take box B, then he has placed you in this one:
Which box should you take?
As mentioned, two reactions are possible. The first is to accept that this is a perfectly legitimate (though unusual) way for the man to offer you a choice between a thousand dollars and a million. If you react in this way, then you will accept that, in choosing between box A and box B, you are indeed choosing between these amounts, and so you will simply take box B and pocket the million. You will not be distracted by the boxes that essentially contain “stones”—the top-right and bottom-left boxes in the diagrams above. These boxes contain 0 and 1,001,000, respectively, but the predictor could have placed just about anything in them without affecting your decision to take box B.
What is the significance of the amounts 0 and 1,001,000? Why did the predictor put those amounts in the “irrelevant” boxes? The answer has to do with the second reaction you might have towards this unusual situation, which is to reject any suggestion that a choice between a thousand dollars and a million is before you. We have already seen why someone might react in this way and I don’t think I need to repeat the explanation here, but we do need to consider what such a person would do if they did react in this way. Which box would they take?
This is the “complication” mentioned above of the daughter who somehow discovers that her father has left one of the boxes empty and objects thereby to the suggestion that the choice between the anklet and the bracelet is really before her. I suppressed this possibility at the time because it would have introduced unnecessary complications into her reaction and behaviour that the father might have been unable to predict. We cannot avoid these complications now since the modus operandi of the predictor is in the open.
And so, which box will you take if you reject the suggestion that a choice between a thousand dollars and a million is before you? The answer of course is that you will take box A, on the “natural” grounds that, whichever situation you are in, box A contains more money than box B. This is the significance of the amounts 0 and 1,001,000 above: they are designed to ensure that box A always contains more money. Notice that, if the predictor had used stones instead, you would no longer have reason to take box A. This is why the version involving stones does not generate Newcomb’s problem in the same way.
This means also that, in order to predict which box you will take, the predictor simply has to anticipate whether you will accept or reject the suggestion that a choice between a thousand dollars and a million has been laid before you.—This, we may suppose, is essentially what the predictor is good at anticipating. We need to put the matter this way because the alternative makes no sense. He cannot predict which box you will take by trying (instead) to anticipate whether you will choose the thousand dollars over the million, or the million dollars over the thousand. That makes no sense because, if you believed that you had that choice, you would of course favour the million. What the predictor is anticipating rather is whether you would believe that you had that choice. Once he foresees this, he can immediately infer whether you will take box A or box B—provided the right amounts are used as “stones.”
The way I see it, the question of whether you should take box A or box B just reduces to the question of whether someone can bestow upon you a choice between a thousand dollars and a million in this rather unusual way. I believe that the answer is “can” and that you should therefore take box B.
Those who reject this answer and favour taking box A will presumably also reject that the girl had the choice between the anklet and the bracelet in the birthday case above. Their view would be that, having neglected to procure the bracelet, her father has robbed her of the choice between the anklet and the bracelet, notwithstanding that he knew that she would not choose the bracelet. Although I think that this view is demonstrably incorrect—and I have tried my best to demonstrate this above—I do not think it is silly. After all, such a distinguished philosopher as David Lewis seems to have held it. These are his words, on behalf of two-boxers in Newcomb’s problem, or A-boxers in the variant above:
We never were given any choice about whether to have a million. When we made our choices, there were no millions to be had. (Lewis 1981, p. 377.)These words are a godsend for my purposes because they encapsulate in a pithy way the essential error I have been labouring to expose: from the mere fact that no millions were to be had, it does not follow that you were never given any choice about whether to have a million.
8. Concluding remarks
So I won’t worry about explaining, for instance, how the analysis can be adapted to the traditional version of Newcomb’s problem, in which you must choose between both boxes and box B, rather than between box A and box B. This sort of detail—and others like it—can be filled in easily by anyone who has read this far.
I should say something however about my use of the word ‘know’ in connection with the predictor’s abilities. I have spoken freely of the predictor knowing which box you will take because this makes it easy to see how something can be among your choices even if it is not there for your taking. Thus, if he knows which box you will take, then it does not matter if he leaves the other box empty, or puts irrelevant stuff in it. This idea does not come across so naturally if the predictor is described in a more precised and nuanced way, e.g., as being likely to have correctly predicted which box you will take.
Nevertheless, the more nuanced way is how Newcomb’s predictor is traditionally described. The talk is in terms of probabilities because this allows us to characterize the predictor’s abilities in a considerably more general way. It also facilitates a mathematical treatment of the issue. So, for instance, the predictor might be said to be 90% accurate, or 60% accurate, or any number in between, and we can ask how varying this number affects the question of which box to take. In contrast, blunt talk of the predictor’s knowing (or not) which box you will take does not adequately address the various possibilities.
So it is fair to ask what happens to our analysis if we speak in terms of probabilities instead? Suppose that the predictor is 90% accurate, in the sense that 90% of one-boxers find him to have predicted their choice correctly, and likewise for two-boxers. (E.g., his track record shows this.) It is your turn to play. Can you continue to think of the choice between a thousand dollars and a million as being before you? Since the predictor sometimes errs, it is not straightforward to say that he knows which box you will take, which was my previous condition for the choice in question to be before you. But he is clearly not just guessing either, so it is not straightforward to say either that you have been robbed of the choice in question. How do we understand what is going on here?
It would take a whole other essay to address this issue properly, but I can easily sketch a meaningful approach here. Imagine facing a predictor who is 90% accurate. Is there a simple way to relate such a predictor to one who knows which box you will take?—If so, we can then avail ourselves of our previous analysis. Well, one way is as follows. Faced with such a predictor, just think of yourself as entering into a gamble in which there is a 90% chance that the predictor knows which box you will take, and a 10% chance that he has bungled it and gotten it wrong. (Other ways are possible but this one is quite simple.) Following our previous analysis, we can then say that there is a 90% chance that, in choosing between box A and box B, you are choosing between a thousand dollars and a million, and a 10% chance that you are choosing instead between whatever “stones” the predictor has placed in the irrelevant boxes. Given the values of the “stones,” we can then calculate which box is better to take. This would normally be done with a traditional expected-utility calculation, which is indeed how one-boxers typically justify their decision to take box B. And so we see that the analysis above is consistent with the traditional way of justifying the decision to take box B.
Two-boxers in Newcomb’s problem typically reject any such calculation because they think (at bottom) that there is no sense in which a choice between a thousand dollars and a million can be said to be before you, as such a calculation implicitly assumes. But once we see the error behind this way of thinking, the traditional calculation seems to me to emerge unscathed. I actually see nothing in Newcomb’s problem which calls traditional expected-utility reasoning into question.
I will leave this sketch there because I am not really concerned to defend the decision to take box B in this essay. To fully defend it would require a substantial excursion into that branch of mathematics and philosophy known as decision theory. I have been concerned rather to give a plain-language account of my struggle with the argument for taking both boxes. I began by saying that I have always been a one-boxer and that Newcomb’s problem (for me) has always been the problem of pinpointing the error in the simple and suasive argument for taking both boxes. Here is a quote from Howard Sobel—a well-known two-boxer—that throws down the gauntlet in exactly the right way:
That this remark was made some thirty years after Newcomb’s problem first surfaced is quite remarkable. Nevertheless, this essay is my response. There is something that “with plausibility” can be said against the case for taking both boxes and I have tried to say it above. It has satisfied me from the moment it struck me and I have never lost a night’s sleep over Newcomb’s problem since then. Wittgenstein once said that while scratching an itch may be a sort of philosophical progress, what one really wants is to be rid of the itch altogether. This answer did it for me and I recommend it to any one-boxer who has yet to overcome his or her conscience. If you remain an unmoved two-boxer, however, I doubt that anything I say could ever move you. I recommend instead a short stint as top chef in the kitchen galley of a major airline!One-boxers of course reject the dominance argument for two-boxing, but they never say what they find wrong with it other than its conclusion. They never explain how, in their views, well-meaning two-boxers are taken in by their arguments … One explanation for it would be that there is nothing wrong with the plain and simple causal-dominance argument for two-boxing, and that there is nothing with plausibility that can be said against it. (Sobel 1998, p. 68.)
References
Martin Gardner (1973), ‘Free Will Revisited, With a Mind-Bending Prediction Paradox by William Newcomb,’ Scientific American, vol. 229, no. 1.
Allan Gibbard & William L. Harper (1978), ‘Counterfactuals and Two Kinds of Expected Utility.’ In C. A. Hooker, J. J. Leach & E. F. McClennen (eds.), Foundations and Applications of Decision Theory, D. Reidel.
Terence Horgan (1981), ‘Counterfactuals and Newcomb’s Problem,’ Journal of Philosophy, vol. 78, no. 6.
________ (1985), ‘Newcomb’s Problem: A Stalemate.’ In Richmond Campbell & Lanning Sowden (eds.), Paradoxes of Rationality and Cooperation: Prisoner’s Dilemma and Newcomb’s Problem, Univ. British Columbia Press.
David Lewis (1981), ‘Why Ain’cha Rich?,’ Noûs, vol. 15, no. 3.
Robert Nozick (1969), ‘Newcomb’s Problem and Two Principles of Choice.’ In Nicholas Rescher (ed.), Essays in Honor of Carl G. Hempel, D. Reidel.
Jordan Howard Sobel (1998), Puzzles For the Will, Univ. Toronto Press.
Menu
What’s a logical paradox?
Achilles & the tortoise
The surprise exam
Newcomb’s problem
Newcomb’s problem (sassy version)
Seeing and being
Logic test!
Philosophers say the strangest things
Favourite puzzles
Books on consciousness
Philosophy videos
Phinteresting
Philosopher biographies
Philosopher birthdays
Draftbarang 2009-2024 
wayback machine
wayback machine