What’s a logical paradox?
Preface
 This was written in 2009. (Revised 2022.) It explains the notion of a logical paradox in a way that comes naturally to me. The conclusion drawn at the end is probably the main thing for me (“We are blinder than we can imagine in matters of straightforward logical reasoning”) but it is not always emphasized by others!
This was written in 2009. (Revised 2022.) It explains the notion of a logical paradox in a way that comes naturally to me. The conclusion drawn at the end is probably the main thing for me (“We are blinder than we can imagine in matters of straightforward logical reasoning”) but it is not always emphasized by others!
 This was written in 2009. (Revised 2022.) It explains the notion of a logical paradox in a way that comes naturally to me. The conclusion drawn at the end is probably the main thing for me (“We are blinder than we can imagine in matters of straightforward logical reasoning”) but it is not always emphasized by others!
This was written in 2009. (Revised 2022.) It explains the notion of a logical paradox in a way that comes naturally to me. The conclusion drawn at the end is probably the main thing for me (“We are blinder than we can imagine in matters of straightforward logical reasoning”) but it is not always emphasized by others!
2. Swallowing the conclusion
 For our first example of an “easily resolved” paradox, imagine that a long rope has been laid snug around the Earth’s equator. (Pretend the Earth is a smooth sphere.)
For our first example of an “easily resolved” paradox, imagine that a long rope has been laid snug around the Earth’s equator. (Pretend the Earth is a smooth sphere.)
It’s an engineering project, say, and the men involved have just finished the job.
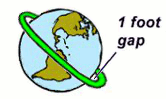 To their chagrin, the foreman now tells them that a mistake has been made. The rope should not lie snug on the ground like that, but should rather be raised one foot above the ground, all the way around. (The reason for this does not matter.)
To their chagrin, the foreman now tells them that a mistake has been made. The rope should not lie snug on the ground like that, but should rather be raised one foot above the ground, all the way around. (The reason for this does not matter.)
Well, in that case, a longer rope will obviously be needed. But roughly how much longer do you think the new rope should be?
A calculation reveals a surprising answer.
The length of the original rope was π × D, where D is the Earth’s diameter. So the length of the new rope must be π × (D + 2), since the diameter has simply expanded by two feet, one on each side. But the difference between these values is simply 2π, which is about 6.28. And so the new rope needs to be only about six feet longer than the old one, which is roughly the height of a man.
Can that be right?
Most people find this result to be very surprising, even “unbelievable.” Surely the new rope must be considerably longer than that? Something on the order of a few miles longer than the old rope would seem to be more appropriate!
And yet the reasoning above is hard to fault: go through it again carefully if necessary!
This is a simple example of a “compelling” piece of reasoning that leads to an “unbelievable” conclusion. The rational mind, as we have seen, cannot tolerate such an abominable tension and will strive to find a resolution. In this example, as I hope you’ll agree, the conclusion does not stay unbelievable for long. Once the reasoning sinks in, the conclusion comes to be accepted: the rope really does need only to be about six feet longer.
This is called “swallowing the conclusion,” and is one of the standard ways to respond to a rational tension of this sort. (The other way is to “reject the reasoning,” which I’ll demonstrate in the next section.) Swallowing the conclusion is clearly the right way to go here since the mathematical reasoning above is beyond question.
Let’s consider another case in which a paradox is quickly resolved by “swallowing the conclusion.” Our next example is often called the birthday paradox and has to do with the following simple question. What are the chances that, in a random group of people, at least two people will have the same birthday?
The answer to this question depends, of course, on how large the group is: the more people there are, the likelier the possibility of a shared birthday. For example, if the group contained just three people, then a shared birthday would be very unlikely, whereas if the group contained 366 people (or more), then it would be absolutely certain that at least two of them would have the same birthday, since there are only 365 birthdays to go around, ignoring leap years for simplicity.
Very well, but now consider this. How large does the group have to be if you merely require there to be an even chance of a shared birthday? (A fifty-fifty chance.) If you’ve never encountered this question before, think about it for a second before reading on. The answer should lie between three and 366, naturally: what do you think a ballpark figure for the size of this group would be?
The birthday paradox is that you need to assemble just twenty-three people to have an even chance of a shared birthday, which is a surprisingly small number! Many people find this hard to believe. Consider the photograph above, for instance, which contains twenty-four people. You’d think that the chances of two of them having the same birthday would be rather low. After all, there are 365 possible birthdays and only twenty-four of them! In fact, however, the chances of a shared birthday between them are greater than even.
The proof of this “unbelievable” result is as follows. Suppose there are N people in the group. Then the probability that all of them have different birthdays is given by this product:
where there are exactly N terms in this product, the first three of which are listed to indicate the pattern. If it’s not evident how this formula is obtained, watch this leisurely explanation from Kevin Lieber.
Notice also that, as N gets larger, the value of the product gets smaller. (The larger the group, the unlikelier it is that everyone will have a different birthday.) Using your dusty, old calculator, you can now easily verify that once N reaches 23, the value of the product falls below ½. At this point, it ceases to be likely that everyone in the group has a different birthday, i.e., a shared birthday is now more likely than not.
The photograph is actually of the attendees of the Fourth Solvay Conference in Physics, held in 1924 in Brussels. I found this photograph at random on the web and was relieved to discover that, indeed, both Marie Curie and Edwin Herbert Hall, seated next to each other in the front row (Hall is holding a hat), have the same birthday of November 7.
The larger point is that this is just another case of a “compelling” piece of reasoning that leads to an “unbelievable” conclusion. The rational mind cannot bear this abominable tension and must either reject the reasoning or swallow the conclusion. In this case, as I hope you’ll again agree, we should swallow the conclusion: despite what may be natural to believe, twenty three people really do suffice for an even chance of a shared birthday. This “resolves the paradox,” as it were.
Let’s now see how we can resolve a paradox in the other way: by “rejecting the reasoning” instead.

It’s an engineering project, say, and the men involved have just finished the job.

Well, in that case, a longer rope will obviously be needed. But roughly how much longer do you think the new rope should be?
A calculation reveals a surprising answer.
The length of the original rope was π × D, where D is the Earth’s diameter. So the length of the new rope must be π × (D + 2), since the diameter has simply expanded by two feet, one on each side. But the difference between these values is simply 2π, which is about 6.28. And so the new rope needs to be only about six feet longer than the old one, which is roughly the height of a man.
Can that be right?
Most people find this result to be very surprising, even “unbelievable.” Surely the new rope must be considerably longer than that? Something on the order of a few miles longer than the old rope would seem to be more appropriate!
And yet the reasoning above is hard to fault: go through it again carefully if necessary!
This is a simple example of a “compelling” piece of reasoning that leads to an “unbelievable” conclusion. The rational mind, as we have seen, cannot tolerate such an abominable tension and will strive to find a resolution. In this example, as I hope you’ll agree, the conclusion does not stay unbelievable for long. Once the reasoning sinks in, the conclusion comes to be accepted: the rope really does need only to be about six feet longer.
This is called “swallowing the conclusion,” and is one of the standard ways to respond to a rational tension of this sort. (The other way is to “reject the reasoning,” which I’ll demonstrate in the next section.) Swallowing the conclusion is clearly the right way to go here since the mathematical reasoning above is beyond question.
⚹
Let’s consider another case in which a paradox is quickly resolved by “swallowing the conclusion.” Our next example is often called the birthday paradox and has to do with the following simple question. What are the chances that, in a random group of people, at least two people will have the same birthday?
The answer to this question depends, of course, on how large the group is: the more people there are, the likelier the possibility of a shared birthday. For example, if the group contained just three people, then a shared birthday would be very unlikely, whereas if the group contained 366 people (or more), then it would be absolutely certain that at least two of them would have the same birthday, since there are only 365 birthdays to go around, ignoring leap years for simplicity.
Very well, but now consider this. How large does the group have to be if you merely require there to be an even chance of a shared birthday? (A fifty-fifty chance.) If you’ve never encountered this question before, think about it for a second before reading on. The answer should lie between three and 366, naturally: what do you think a ballpark figure for the size of this group would be?
The birthday paradox is that you need to assemble just twenty-three people to have an even chance of a shared birthday, which is a surprisingly small number! Many people find this hard to believe. Consider the photograph above, for instance, which contains twenty-four people. You’d think that the chances of two of them having the same birthday would be rather low. After all, there are 365 possible birthdays and only twenty-four of them! In fact, however, the chances of a shared birthday between them are greater than even.
The proof of this “unbelievable” result is as follows. Suppose there are N people in the group. Then the probability that all of them have different birthdays is given by this product:
\( \frac{365}{365} \times \frac{364}{365} \times \frac{363}{365} \times \ldots \) (N terms)
where there are exactly N terms in this product, the first three of which are listed to indicate the pattern. If it’s not evident how this formula is obtained, watch this leisurely explanation from Kevin Lieber.
Notice also that, as N gets larger, the value of the product gets smaller. (The larger the group, the unlikelier it is that everyone will have a different birthday.) Using your dusty, old calculator, you can now easily verify that once N reaches 23, the value of the product falls below ½. At this point, it ceases to be likely that everyone in the group has a different birthday, i.e., a shared birthday is now more likely than not.
The photograph is actually of the attendees of the Fourth Solvay Conference in Physics, held in 1924 in Brussels. I found this photograph at random on the web and was relieved to discover that, indeed, both Marie Curie and Edwin Herbert Hall, seated next to each other in the front row (Hall is holding a hat), have the same birthday of November 7.
The larger point is that this is just another case of a “compelling” piece of reasoning that leads to an “unbelievable” conclusion. The rational mind cannot bear this abominable tension and must either reject the reasoning or swallow the conclusion. In this case, as I hope you’ll again agree, we should swallow the conclusion: despite what may be natural to believe, twenty three people really do suffice for an even chance of a shared birthday. This “resolves the paradox,” as it were.
Let’s now see how we can resolve a paradox in the other way: by “rejecting the reasoning” instead.
Menu
 What’s a logical paradox?
What’s a logical paradox? Achilles & the tortoise
Achilles & the tortoise The surprise exam
The surprise exam Newcomb’s problem
Newcomb’s problem Newcomb’s problem (sassy version)
Newcomb’s problem (sassy version) Seeing and being
Seeing and being Logic test!
Logic test! Philosophers say the strangest things
Philosophers say the strangest things Favourite puzzles
Favourite puzzles Books on consciousness
Books on consciousness Philosophy videos
Philosophy videos Phinteresting
Phinteresting Philosopher biographies
Philosopher biographies Philosopher birthdays
Philosopher birthdays Draft
Draftbarang 2009-2024  wayback machine
wayback machine
 wayback machine
wayback machine

