9. Thomson’s lamp
Consider a lamp which may be easily toggled on and off.
The lamp is first off, but half a second later, toggled on. A quarter of a second later, off. After another eighth, back on. This shuttle continues endlessly, with the toggle time halved each time:
Notice that the numbers on the left edge ever closer towards 1, but never quite reach it. So the lamp flashes on and off ever faster as one second approaches, without end.
Of course, no actual lamp could exhibit this fantastic behaviour, but it is enough just to imagine one.
 The philosopher James Thomson asked whether the lamp would be on or off after exactly one second. What should we say?
The philosopher James Thomson asked whether the lamp would be on or off after exactly one second. What should we say?
At first sight, the question seems impossible to answer. Since the lamp shuttles on and off ever faster as one second approaches, there’s no saying in which state it will be at exactly one second. Either answer seems arbitrary.
But a nuanced answer is possible.
Notice that the table reveals the state of the lamp at all moments prior to one second, but is silent on the state of the lamp at exactly one second, or beyond. So the nuanced answer is that we haven’t been given enough information! The lamp could be in any state at exactly one second, consistent with the information found in the table.
This answer is correct, so far as it goes, but there is still something puzzling about Thomson’s lamp.
Since the lamp may be in any state at one second, let’s suppose it is off. Then the lamp will be flashing ever faster prior to one second, and then it will be off. This may seem to involve no contradiction, but it does engender a certain awkward “disjoint” at exactly one second, when the lamp goes off.
Consider a graph of the lamp’s state prior to one second:
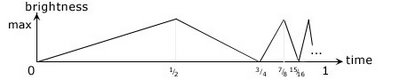
To make sense of the graph, imagine that the lamp slides between minimum and maximum brightness ever faster as one second approaches, endlessly. (This is how it would normally have to be, of course.)
If we now add the information that the lamp is off at one second, it proves impossible to “connect” this with the existing information:
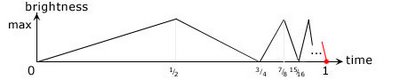
Thus, the red dot denotes the lamp being off at one second and the red line attempts to connect this to the existing graph. But this is impossible, since the black line oscillates endlessly.
So we cannot explain how the lamp came to be off, in terms of anything that happened moments before. In particular, we cannot say that its illuminance decreased (however rapidly) from a state of maximum brightness down to zero. There is simply no connection between the state of the lamp at one second and any of its previous states.
All we can say is that the lamp was flashing ever faster, and then it was off. Or perhaps on. Or, indeed, at any other level of brightness whatever. It does not matter, because God might just as well have created the whole lamp anew at exactly one second in a random state of luminance.
This is the awkward “disjoint” at one second referred to above. It may be what people sense is also present with Achilles at the doorway, and the root of their discomfort with that problem. As before, the matter does not concern time. The difficulty is not how a lamp can oscillate endlessly within one second. It lies rather with the disjoint transition that occurs at the end of that second.
We have used Thomson’s lamp to illustrate this strange disjoint and should now ask if it also infects Achilles at the instant he breaches the doorway. And would it matter if it did?
Consider a lamp which may be easily toggled on and off.
The lamp is first off, but half a second later, toggled on. A quarter of a second later, off. After another eighth, back on. This shuttle continues endlessly, with the toggle time halved each time:
| Seconds after start | State of lamp |
| 0 | off |
| 1⁄2 | on |
| 3⁄4 | off |
| 7⁄8 | on |
| 15⁄16 | off |
| ⋮ | ⋮ |
Notice that the numbers on the left edge ever closer towards 1, but never quite reach it. So the lamp flashes on and off ever faster as one second approaches, without end.
Of course, no actual lamp could exhibit this fantastic behaviour, but it is enough just to imagine one.

At first sight, the question seems impossible to answer. Since the lamp shuttles on and off ever faster as one second approaches, there’s no saying in which state it will be at exactly one second. Either answer seems arbitrary.
But a nuanced answer is possible.
Notice that the table reveals the state of the lamp at all moments prior to one second, but is silent on the state of the lamp at exactly one second, or beyond. So the nuanced answer is that we haven’t been given enough information! The lamp could be in any state at exactly one second, consistent with the information found in the table.
This answer is correct, so far as it goes, but there is still something puzzling about Thomson’s lamp.
Since the lamp may be in any state at one second, let’s suppose it is off. Then the lamp will be flashing ever faster prior to one second, and then it will be off. This may seem to involve no contradiction, but it does engender a certain awkward “disjoint” at exactly one second, when the lamp goes off.
Consider a graph of the lamp’s state prior to one second:

To make sense of the graph, imagine that the lamp slides between minimum and maximum brightness ever faster as one second approaches, endlessly. (This is how it would normally have to be, of course.)
If we now add the information that the lamp is off at one second, it proves impossible to “connect” this with the existing information:

Thus, the red dot denotes the lamp being off at one second and the red line attempts to connect this to the existing graph. But this is impossible, since the black line oscillates endlessly.
So we cannot explain how the lamp came to be off, in terms of anything that happened moments before. In particular, we cannot say that its illuminance decreased (however rapidly) from a state of maximum brightness down to zero. There is simply no connection between the state of the lamp at one second and any of its previous states.
All we can say is that the lamp was flashing ever faster, and then it was off. Or perhaps on. Or, indeed, at any other level of brightness whatever. It does not matter, because God might just as well have created the whole lamp anew at exactly one second in a random state of luminance.
This is the awkward “disjoint” at one second referred to above. It may be what people sense is also present with Achilles at the doorway, and the root of their discomfort with that problem. As before, the matter does not concern time. The difficulty is not how a lamp can oscillate endlessly within one second. It lies rather with the disjoint transition that occurs at the end of that second.
We have used Thomson’s lamp to illustrate this strange disjoint and should now ask if it also infects Achilles at the instant he breaches the doorway. And would it matter if it did?
Menu
 What’s a logical paradox?
What’s a logical paradox? Achilles & the tortoise
Achilles & the tortoise The surprise exam
The surprise exam Newcomb’s problem
Newcomb’s problem Newcomb’s problem (sassy version)
Newcomb’s problem (sassy version) Seeing and being
Seeing and being Logic test!
Logic test! Philosophers say the strangest things
Philosophers say the strangest things Favourite puzzles
Favourite puzzles Books on consciousness
Books on consciousness Philosophy videos
Philosophy videos Phinteresting
Phinteresting Philosopher biographies
Philosopher biographies Philosopher birthdays
Philosopher birthdays Draft
Draftbarang 2009-2024  wayback machine
wayback machine
 wayback machine
wayback machine
 Written in 2009.
Written in 2009. What Is the Answer to Zeno’s Paradox? (2014), by Brian Palmer.
What Is the Answer to Zeno’s Paradox? (2014), by Brian Palmer.