5. Curious infinite sums

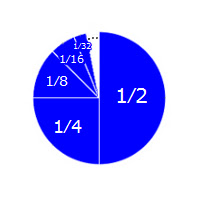Imagine a pie, infinitely sliced as shown.

The first slice is half of the pie, the second a quarter, the third an eighth, and so on, without end.

If we add up all the slices, we will obviously get one whole pie! So, curiously, the answer to our infinite sum is actually 1:

¹⁄₂ + ¹⁄₄ + ¹⁄₈ + ¹⁄₁₆ + ¹⁄₃₂ + …   =   1

This equation is amazing. Since the sum keeps increasing without end, one would expect it to blow up to infinity. But the pie shows otherwise and here’s another nice example:Here too the sum increases endlessly but the result is obviously correct. So, amazingly, an infinity of positive numbers can sum to a finite quantity.

Of course, many infinite sums do blow up to infinity, such as these:

1 + 2 + 3 + 4 + …   =   ∞

¹⁄₂ + ¹⁄₂ + ¹⁄₂ + ¹⁄₂ + …  =   ∞

But this is not always true and, indeed, the result of an infinite sum is not always predictable.

From our examples, it may seem that if the individual numbers decrease as the sequence progresses, the result won’t blow up to infinity, but it’s not that simple, as this famous example shows:

¹⁄₂ + ¹⁄₃ + ¹⁄₄ + ¹⁄₅ + …   =   ∞

We can’t prove this (well-known) result here, but such infinite sums have been investigated by mathematicians for centuries, with the full fruit of their labours being realized only in the 19th century.

For our purposes, it suffices to have vindicated Achilles. As we saw, these two facts about Achilles cannot be denied:

To reach the doorway, Achilles must undertake an infinite sequence of movements.

 

Each movement will occupy some of his time.

But it does not follow that, to complete the undertaking, Achilles requires an infinite amount of time.

In terms of our example, that would follow only if this equation were correct:

¹⁄₂ + ¹⁄₄ + ¹⁄₈ + ¹⁄₁₆ + ¹⁄₃₂ + …   =   ∞

But we saw that this is wrong; the correct sum is actually 1.

Indeed, in our example, Achilles stands one meter from the doorway and walks at one meter per second. So we would expect him to take one second to reach the doorway. The correct infinite sum fully bears this out.

The question now is whether this resolves the paradox.