11. Hop, step and shuffle
Imagine, for a moment, that Achilles decides to step through Zeno’s sequence of points. Right foot, then left, every point along the way. Towards the end, we find him shuffling rapidly towards the doorway.

Everything else is the same – he takes half a second to reach point 2, another quarter of a second to reach point 3, and so on, throughout the sequence.
Many people readily think in these terms, as they contemplate Achilles moving through Zeno’s points. They treat each pointwise movement as a unit and pair it with some familiar unit of bodily motion. (Hopping through the points will also do.)
Of course, we could simply think in the normal way, with Achilles walking steadily towards the doorway, but many gravitate to this alternative mode of thinking, especially when contemplating the problem in slow motion.
Assuming that Achilles can hop, step or shuffle sufficiently fast, the problem seems unchanged, since the essential thing is that he moves from point to point in the required time, and not how he does so. Indeed, one thinks that he may even pause briefly at each point, so long as he gets to the next one in time.
 Unfortunately, however, these natural thoughts are disastrous, because in redrawing the problem this way, we unwittingly reduce it to the case of the man and the pie and open ourselves up to the awaiting bodily disjoint!
Unfortunately, however, these natural thoughts are disastrous, because in redrawing the problem this way, we unwittingly reduce it to the case of the man and the pie and open ourselves up to the awaiting bodily disjoint!
Thus, after exactly one second, Achilles is at the doorway. But in what position is his right leg (say) at this exact instant? How did it get to be in that position? Or if he is hopping through the points, how high is he off the ground at the instant he crosses the doorway?
As we know, no answers are forced upon us. All answers are permitted. No matter how his right leg is positioned when he crosses the doorway, it will be disjoint from its prior states of motion, in the way previously explained. And so we must imagine Achilles “popping out” of Zeno’s sequence after exactly one second in some random bodily state disconnected from his previous ones, and being perplexed over how that can be.
In contrast, if we imagine Achilles walking towards the doorway in the normal way, the difficulty does not arise. His body and limbs will transit past the doorway as smoothly as his center of gravity does, and no disjoint of the sort in question will surface.
We may illustrate the difference with Achilles’s right leg. Whether he steps through the points, or just walks normally, his leg will repeatedly assume a range of different positions. Consider these three, and the obvious ones in between:

The following diagrams illustrate how his leg will repeatedly cycle through these positions, depending on his gait:
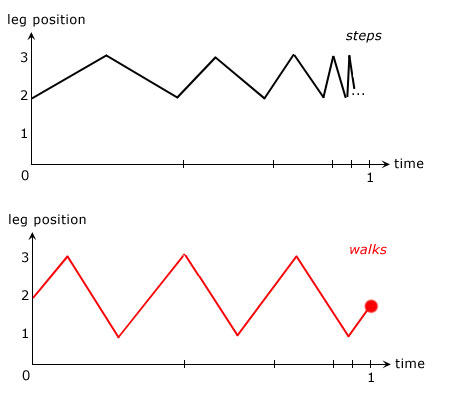
If he steps from point to point, his leg cycles ever more rapidly as one second nears, rendering its position at one second indeterminate, thereby raising the problem. But if he just walks normally, his leg will cycle in a much more regular way and its position at one second will be smoothly determined. (Red dot.)
So the Achilles hop, step or shuffle is not as innocuous as it first looks! On the contrary, it is quite disastrous to redraw Zeno’s problem in that way. If Achilles just walks in the normal way, the dreaded bodily disjoint will not arise.
We need not worry about whether Achilles can get through the doorway with one of the alternate gaits just mentioned. It certainly isn’t humanly possible for him to do so, since, beyond a point, the hop, step or shuffle cannot be performed that fast. A philosopher might wonder if it is nevertheless logically possible for him to do so, but this is like asking about the man and the pie, and need not detain us here!
So we have removed yet another barrier between Achilles and the doorway. The vaguely perceived difficulty with the endlessness of Zeno’s sequence proved to be quite genuine but it can also be addressed. The problem doesn’t really arise, after all, but we can see why one might unwittingly think that it does, especially if one contemplates the problem in slow motion!
There are likely to be hidden depths in Zeno’s problem but I hope that the above has yielded some idea of how to tackle such a fiendish problem. Everything we have said applies just as well to Achilles and the tortoise, so we might usefully sum everything up in those terms.
Imagine, for a moment, that Achilles decides to step through Zeno’s sequence of points. Right foot, then left, every point along the way. Towards the end, we find him shuffling rapidly towards the doorway.

Everything else is the same – he takes half a second to reach point 2, another quarter of a second to reach point 3, and so on, throughout the sequence.
Many people readily think in these terms, as they contemplate Achilles moving through Zeno’s points. They treat each pointwise movement as a unit and pair it with some familiar unit of bodily motion. (Hopping through the points will also do.)
Of course, we could simply think in the normal way, with Achilles walking steadily towards the doorway, but many gravitate to this alternative mode of thinking, especially when contemplating the problem in slow motion.
Assuming that Achilles can hop, step or shuffle sufficiently fast, the problem seems unchanged, since the essential thing is that he moves from point to point in the required time, and not how he does so. Indeed, one thinks that he may even pause briefly at each point, so long as he gets to the next one in time.

Thus, after exactly one second, Achilles is at the doorway. But in what position is his right leg (say) at this exact instant? How did it get to be in that position? Or if he is hopping through the points, how high is he off the ground at the instant he crosses the doorway?
As we know, no answers are forced upon us. All answers are permitted. No matter how his right leg is positioned when he crosses the doorway, it will be disjoint from its prior states of motion, in the way previously explained. And so we must imagine Achilles “popping out” of Zeno’s sequence after exactly one second in some random bodily state disconnected from his previous ones, and being perplexed over how that can be.
In contrast, if we imagine Achilles walking towards the doorway in the normal way, the difficulty does not arise. His body and limbs will transit past the doorway as smoothly as his center of gravity does, and no disjoint of the sort in question will surface.
We may illustrate the difference with Achilles’s right leg. Whether he steps through the points, or just walks normally, his leg will repeatedly assume a range of different positions. Consider these three, and the obvious ones in between:

The following diagrams illustrate how his leg will repeatedly cycle through these positions, depending on his gait:

If he steps from point to point, his leg cycles ever more rapidly as one second nears, rendering its position at one second indeterminate, thereby raising the problem. But if he just walks normally, his leg will cycle in a much more regular way and its position at one second will be smoothly determined. (Red dot.)
So the Achilles hop, step or shuffle is not as innocuous as it first looks! On the contrary, it is quite disastrous to redraw Zeno’s problem in that way. If Achilles just walks in the normal way, the dreaded bodily disjoint will not arise.
We need not worry about whether Achilles can get through the doorway with one of the alternate gaits just mentioned. It certainly isn’t humanly possible for him to do so, since, beyond a point, the hop, step or shuffle cannot be performed that fast. A philosopher might wonder if it is nevertheless logically possible for him to do so, but this is like asking about the man and the pie, and need not detain us here!
So we have removed yet another barrier between Achilles and the doorway. The vaguely perceived difficulty with the endlessness of Zeno’s sequence proved to be quite genuine but it can also be addressed. The problem doesn’t really arise, after all, but we can see why one might unwittingly think that it does, especially if one contemplates the problem in slow motion!
There are likely to be hidden depths in Zeno’s problem but I hope that the above has yielded some idea of how to tackle such a fiendish problem. Everything we have said applies just as well to Achilles and the tortoise, so we might usefully sum everything up in those terms.
Menu
 What’s a logical paradox?
What’s a logical paradox? Achilles & the tortoise
Achilles & the tortoise The surprise exam
The surprise exam Newcomb’s problem
Newcomb’s problem Newcomb’s problem (sassy version)
Newcomb’s problem (sassy version) Seeing and being
Seeing and being Logic test!
Logic test! Philosophers say the strangest things
Philosophers say the strangest things Favourite puzzles
Favourite puzzles Books on consciousness
Books on consciousness Philosophy videos
Philosophy videos Phinteresting
Phinteresting Philosopher biographies
Philosopher biographies Philosopher birthdays
Philosopher birthdays Draft
Draftbarang 2009-2024  wayback machine
wayback machine
 wayback machine
wayback machine
 Written in 2009.
Written in 2009. What Is the Answer to Zeno’s Paradox? (2014), by Brian Palmer.
What Is the Answer to Zeno’s Paradox? (2014), by Brian Palmer.