1. The problem


Newcomb’s problem is named after the American physicist William Newcomb who discovered it in the 1960s while thinking about the prisoner’s dilemma.

The Harvard philosopher Robert Nozick wrote an extended essay on the problem in 1969, describing it carefully and isolating the precise difficulty. This seminal paper, ‘Newcomb’s Problem and Two Principles of Choice,’ is widely regarded as the classic introduction to the issue.

Martin Gardner helped popularize the problem through two of his Mathematical Games columns for Scientific American in 1973 and 1974. (He invited Nozick to write the second column.) These lively columns constitute one of the best, short introductions to the problem.

Nevertheless, after forty years, the issue remains largely confined to academic circles and is not as well-known as it deserves to be.

Briefly put, Newcomb’s problem is a decision problem. A certain situation is described and you must decide which of two choices open to you is the better one to make. The trouble is that each choice has something rather convincing to be said for it, which is why some call this Newcomb’s paradox.

Here’s the situation.

Two boxes, A and B, stand before you. You know that A contains $1,000 for sure, while B contains either $1,000,000 or nothing, though you don’t know which.


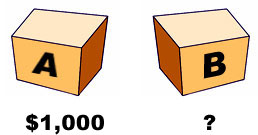
You have a choice between taking both boxes or just box B, where you may keep whatever you find in the box or boxes that you take. (The contents of box B will not be revealed until you have made your choice.)

The boxes are sealed and there is no question of their contents being tampered with. Indeed, since, on either choice, you must take box B, you may take it away now for safekeeping, though without opening it yet. The question therefore is whether you want to take box A as well, which you know to contain $1,000. (You may open box A to verify this.)

Why is this a problem? If your sole aim is money, as we may suppose, why not take both boxes and be done with it?

The catch is that the contents of box B depend on what a certain man predicted (beforehand) you would do. This man is a skilled psychologist, say, and known to be very good at anticipating people’s choices. Moreover, if he predicted that you would take just box B, he has left the million dollars in it, but if he predicted that you would take both boxes (or do anything else), he has left box B empty.

His prediction was made yesterday (or even a week beforehand) and the contents of box B have long been settled and may no longer change. You are informed of all this and he knew that you would be so informed.

You have every indication that this man is likely to have predicted your choice correctly, though, of course, there is no way to be absolutely sure of this. While he is a very good predictor, with a very good record of correct predictions, he is known to slip up once in a while. Nevertheless, you tend to believe (with good reason) that he has predicted your choice correctly. Put another way, it’s a good bet that he has.

If your sole aim is money, should you take both boxes or just box B? This is Newcomb’s problem.